Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » funkcia 2 premenných so zaujímavou vlastnosťou (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 10. 2014 10:55
funkcia 2 premenných so zaujímavou vlastnosťou
ahojte môže existovať reálna funkcia dvoch reálnych premenných taká , že
teda že dvojná limita (relatívna k oboru definície) neexistuje, ale po každej spojitej ceste sú limity rovnaké
čiže pokazí sa to len v úplne všeobecnom prípade premenných x,y?
MATH IS THE BEST!!!
Offline
- (téma jako vyřešené označil(a) jarrro)
#2 06. 10. 2014 11:09
Re: funkcia 2 premenných so zaujímavou vlastnosťou
↑ jarrro:
Ahoj.
Tvoje formálně vyjádřená podmínka neuvažuje cestu po ose y. Ale to by se snadno dalo vyřešit křivkami
popsanými pomocí parametrických rovnic. Řešení problému při tomto zpřísnění mne ale (zatím ?) nenapadá.
Offline
#3 06. 10. 2014 11:43
Re: funkcia 2 premenných so zaujímavou vlastnosťou
↑ Rumburak:aha čiže zápis by potom bol
?
MATH IS THE BEST!!!
Offline
#6 07. 10. 2014 11:52
Re: funkcia 2 premenných so zaujímavou vlastnosťou
↑ jarrro:
Domnívám se, že taková funkce  neeexistuje. Připadá mi, že ta Tvoje podmínka s cestami po křivkách
neeexistuje. Připadá mi, že ta Tvoje podmínka s cestami po křivkách
je analogická podmínce z Heineho věty.
Když bychom měli posloupnost  bodů roviny různých od počátku
bodů roviny různých od počátku  a takovou, že
a takovou, že 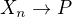 , př čemž
, př čemž 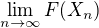 by neexistovata, pak by nemohla existiovat ani limita funkce
by neexistovata, pak by nemohla existiovat ani limita funkce  po lomené čáře
po lomené čáře 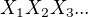
(k posloupnosti  můžeme případně přidat i další body tak, aby při dodržení podmínky
můžeme případně přidat i další body tak, aby při dodržení podmínky 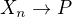
žádná z úseček 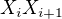 neprocházela počátkem .)
neprocházela počátkem .)
Offline
#7 07. 10. 2014 14:51 — Editoval jarrro (08. 10. 2014 10:00)
Re: funkcia 2 premenných so zaujímavou vlastnosťou
↑ Rumburak:aha díky to ma nenapadlo teda vlastne každá postupnosť bodov sa dá vnoriť do spojitej cesty
čiže z rovnosti limít na každej spojitej ceste vyplýva rovnosť limít na každej rovnako limitnej postupnosti
MATH IS THE BEST!!!
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » funkcia 2 premenných so zaujímavou vlastnosťou (TOTO TÉMA JE VYŘEŠENÉ)
