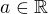Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 08. 04. 2009 21:23
- marnes

- Příspěvky: 11227
Re: rovnice kružnice
↑ kukulkan:
Dosaď do obecné rovnice body A a B. Budeš mít dvě rovnice o neznámých xs a ys - souřadnice středu,, pak použiješ poslední info, ato že leží S na ose x, tzn, že ys=0. Vypočítáš xs. Poloměr je pak vzdálenost třeba AS
Jo. A na začátku vás zdravím.
Offline
#4 08. 04. 2009 21:25
Re: rovnice kružnice
středová rovnice kružnice: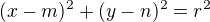
Střed kružnice je průsečíkem osy x a osy (označíme např. jako přímku q) úsečky AB . Středem úsečky AB je bod P[\frac{5+7}{2},\frac{4+0}{2}]=[6;2]. Pro směrnice přímky q a úsečky AB platí 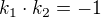

Přímka q (osa úsečky AB) má rovnici 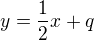 a prochází bodem
a prochází bodem ![kopírovat do textarea $P[6;2]$](/mathtex/8e/8e80427eac4c4dc082dc96f71709d81a.gif) :
: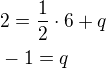
Vyřešíme průsečík přímky q: 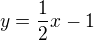 a osy x:
a osy x: 
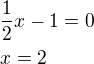
Souřadnice středu kružnice jsou ![kopírovat do textarea $S[2;0]$](/mathtex/22/224b82245f22cae321575489333a8ece.gif) .
.
Poloměr kružnice 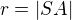
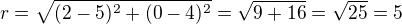
Rovnice kružnice: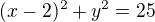
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#5 09. 04. 2009 07:09
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: rovnice kružnice
↑ kukulkan:
Tady snad na doplnění obrázek
http://forum.matweb.cz/upload/500-aa.JPG
Nikdo není dokonalý
Offline
#6 27. 11. 2009 15:30
Re: rovnice kružnice
prosím o pomoc s příkladem, kdy se majá v závislosti na parametru a vyjádřit průsečíky přímky p: y = ax +a s kružnicí k: x na 2 + y na 2 = 1. Já jsem si napřed dosadila p do k a vyšla mi kvadratická rovnice s tím parametrem a. Ale nevím, jak teď dál postupovat, abych našla všechny průsečíky. Prosím poraďte mi. děkuji
Offline
![kopírovat do textarea $A=[5;4]$](/mathtex/59/593f2daddc388fab70e1fbe8bad7c13d.gif)
![kopírovat do textarea $B=[7;0]$](/mathtex/0f/0f2b62e6bc3b5fe7e0fa510103e70b51.gif)
![kopírovat do textarea $S=[n;0]$](/mathtex/20/20b4d7f56fda3ae2bba930218721c441.gif)
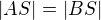
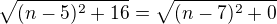
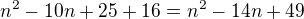
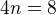
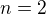
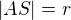
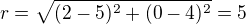
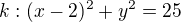

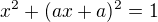
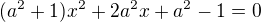
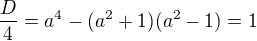
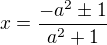

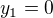
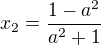 ,
,