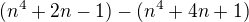Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
![$\lim_{n\to \infty } \frac{1}{\sqrt[4]{n^{4} + 2n -1} - \sqrt[4]{n^{4} + 4n + 1}}$](/mathtex/51/51802a19291e2f5a7d69f11c745755fd.gif "kopírovat do textarea")
![$\ \frac{1}{\sqrt[4]{n^{4} + 2n -1} - \sqrt[4]{n^{4} + 4n + 1}}*\frac{\sqrt[4]{n^{4} + 2n -1} + \sqrt[4]{n^{4} + 4n + 1}}{\sqrt[4]{n^{4} + 2n -1} + \sqrt[4]{n^{4} + 4n + 1}}*\frac{\sqrt[2]{n^{2} + 2n -1} + \sqrt[2]{n^{4} + 4n + 1}}{\sqrt[2]{n^{4} + 2n -1} + \sqrt[2]{n^{4} + 4n + 1}}$](/mathtex/35/35f8cf616c7bbc080293aef5e0a93606.gif "kopírovat do textarea")
, což dá![$\ \frac{\sqrt[4]{n^{4} + 2n -1} + \sqrt[4]{n^{4} + 4n + 1}}{\sqrt[2]{n^{4} + 2n -1} -\sqrt[2]{n^{4} + 4n + 1}}*\frac{\sqrt[2]{n^{2} + 2n -1} + \sqrt[2]{n^{4} + 4n + 1}}{\sqrt[2]{n^{4} + 2n -1} + \sqrt[2]{n^{4} + 4n + 1}}$](/mathtex/22/2222b35bf29843566d23cb2b12eb8721.gif "kopírovat do textarea")
a dál už to jde vidět.![$\frac{\sqrt[4]{n^{4} + 2n -1} + \sqrt[4]{n^{4} + 4n + 1}}{\sqrt[2]{n^{4} + 2n -1} -\sqrt[2]{n^{4} + 4n + 1}}*\frac{\sqrt[2]{n^{2} + 2n -1} + \sqrt[2]{n^{4} + 4n + 1}}{\sqrt[2]{n^{4} + 2n -1} + \sqrt[2]{n^{4} + 4n + 1}}$](/mathtex/86/867a720f7c4ecb284993d51b2135a3da.gif "kopírovat do textarea")
![$\frac{\sqrt[4]{n^{4} + 2n -1} + \sqrt[4]{n^{4} + 4n + 1}}{{(n^{4} + 2n -1)} -{(n^{4} + 4n + 1)}}*\frac{\sqrt[2]{n^{2} + 2n -1} + \sqrt[2]{n^{4} + 4n + 1}}{\sqrt[2]{n^{\color{red}2} + 2n -1} + \sqrt[2]{n^{4} + 4n + 1}}$](/mathtex/00/0020e3737ecd41ed25abf4f84599da58.gif "kopírovat do textarea")
![$\frac{\sqrt[2]{n^{\color{red}4} + 2n -1} + \sqrt[2]{n^{4} + 4n + 1}}{\sqrt[2]{n^{4} + 2n -1} + \sqrt[2]{n^{4} + 4n + 1}}$](/mathtex/b8/b8cceed9365ca6c36f4f5bbc3264d795.gif "kopírovat do textarea")
, takže ten tvůj poslední výraz má být![$\frac{\sqrt[4]{n^{4} + 2n -1} + \sqrt[4]{n^{4} + 4n + 1}}{{(n^{4} + 2n -1)} -{(n^{4} + 4n + 1)}}*\frac{\sqrt[2]{n^{\color{red}4} + 2n -1} + \sqrt[2]{n^{4} + 4n + 1}}{1}$](/mathtex/ac/acfd5e615b6c4f5c7742d35b21c8072e.gif "kopírovat do textarea")
![$\sqrt[2]{n^{4} + 2n -1} + \sqrt[2]{n^{4} + 4n + 1}$](/mathtex/20/2024bc2a9e39b823e3486db5d53d9091.gif "kopírovat do textarea")
z jmenovatele a v jmenovateli pak už zůstalo jen 