Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#7 13. 11. 2014 11:54 — Editoval vanok (13. 11. 2014 11:55)
Re: súčet radu
Poznamka
Keby si nepreskakoval etapy a zacal napr takto  Atd.
Atd.
A tiez ak by sipoznamenal ze ide o geometricky rad.... Korektor by ti gratuloval za kvalitu riesenia.( vzdy treba vysvetlit slovne co robis, inac tvoje myslienky mozu byt neuznane)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 13. 11. 2014 13:20
Re: súčet radu
Ahoj ↑ Brano:
Ale ako sa zda korektor nepochopil myslienkovy postup, tak som navrhol lopàtisticku formu rIesenia. ( alebo ide o hyperformalistickeho cloveka, a o sa mu neda vycitat.😄)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 13. 11. 2014 13:52
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: súčet radu
ahoj ↑ vizdo:,
jak říká kolega ↑ Brano:, máš to dobře, jenom trochu komplikovaně. Postup zjednodušil kolega ↑ vanok:, já bych udělal ještě dva kroky, abych to ještě zpolopatoval:
jelikož ta mínus jednička je vždy umocněna na sudé číslo. Takže bych to učiteli ukázal a on by měl na svoji opravu změnit názor :-)
Budoucnost patří aluminiu.
Offline
#11 13. 11. 2014 16:05 — Editoval Brano (13. 11. 2014 16:07)
Re: súčet radu
↑ Eratosthenes:
to je tak trocha aj vec vkusu; mne sa napriklad zda postup OP jednoduchsi (v zmysle nazornejsi) ako tvoj, ale to nie je velmi podstatne pri takto jednoduchom priklade
↑ vizdo:
tak ci tak treba sa toho co to opravoval spytat co mu vlastne vadilo, lebo daju sa robit vselijake teoreticke vysvetlenia, ale najpravdepodobnejsie mi pripada proste to, ze sa ten co to opravoval proste pomylil; vsetci sme ludia a robime chyby
Offline


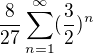


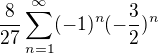
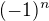 ? Bude se tam střídat znaménko +-+-+-...
? Bude se tam střídat znaménko +-+-+-...