Matematické Fórum

janca361 · 16. 11. 2014 22:15

Ahoj, mám následující příklad:
Ověřte, že vektory 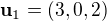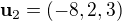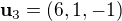$\mathbf{u}_1=(3,0,2)$ , $\mathbf{u}_2=(-8,2,3)$ , $\mathbf{u}_3=(6,1,-1)$ tvoří bázi 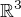$\mathbb{R}^3$ a nalezněte souřadnice vektoru 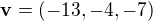$\mathbf{v}=(-13,-4,-7)$ v této bázi.

Výsledkem by mělo být: 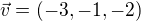$\vec{v}=(-3,-1,-2)$

Postupovala jsem následovně...
$\left( \begin{array}{ccc@{\ }r} 3 & -8 & 6 & -13\\ 0 & 2 & 1 & -4\\ 2 & 3 & -1 & -7\\ \end{array} \right) \sim \ldots \sim \left( \begin{array}{ccc@{\ }r} -2 & 3 & 2 & -13\\ 0 & 2 & 1 & -4\\ 0 & 0 & 1 & -2\\ \end{array} \right)$
... a výsledek mi nějak nesedí. Netuším zda postupuju dobře nebo jen neumím počítat. (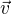 $\vec{v}$ je v mém případě $(-13,-4,-2)$ )

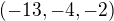Poradí mi ěkdo jak se dobrat k výsledku?
Díky.

misaH · 16. 11. 2014 22:33 — Editoval misaH (16. 11. 2014 22:45)

↑ janca361:

Poslednú maticu treba upraviť na tvar s jednotkami na diagonále a ináč samými nulami.

Ale prvý riadok má byť ten pôvodný 3 -8 6 - 13.

janca361

↑ misaH:
I tak mi to nevychází...

$\left( \begin{array}{ccc@{\ }r} 3 & -8 & 6 & -13\\ 0 & 2 & 1 & -4\\ 0 & 0 & 1 & -2\\ \end{array} \right) \sim \ldots \sim \left( \begin{array}{ccc@{\ }r} 3 & 0 & 0 & 13\\ 0 & 1 & 0 & -1\\ 0 & 0 & 1 & -2\\ \end{array} \right) \sim \left( \begin{array}{ccc@{\ }r} 1 & 0 & 0 & 13/3\\ 0 & 1 & 0 & -1\\ 0 & 0 & 1 & -2\\ \end{array} \right)$

... ale zkusím to spočítat znovu, třeba někde bude numerická chyba.

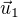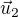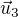A ještě dotaz.. kdyby tam bylo jen "obvěřtem zda $\vec{u}_1$ , $\vec{u}_2$ a $\vec{u}_3$ tvoří bázi $\mathbb{R}^3$ "

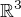Tak jak na to?
Přes
$\left( \begin{array}{ccc@{\ }r} 3 & -8 & 6 \\ 0 & 2 & 1 \\ 2 & 3 & -1\\ \end{array} \right)$
a v jednotlivých sloupcích musí být pivoty, tj. musí být vektory lineárně nezávislé?

misaH · 16. 11. 2014 22:59 — Editoval misaH (16. 11. 2014 23:04)

↑ janca361:

Keď dávaš preč 6 v prvom riadku, násobok posledný číslom -6.

Dostaneš 3 -8 0 -1.

Podľa mňa stačí lineárna nezávislosť 3 vektorov v 3D.

janca361 · 16. 11. 2014 23:12

Celý můj postup:
//forum.matweb.cz/upload3/img/2014-11/75866_20141116_230630.jpg
Já chybu nevidím (ale asi tam bude)

misaH · 16. 11. 2014 23:16

↑ janca361:

No - minimálne v prvom riadku má byť -13.

vanok · 16. 11. 2014 23:29

Poznamka:
Metod na dokaz LN tvojich 3 vektorov je spusta.
Tvoja myslienka GEM je tiez pouzitelna.
Rychlo dostanes;
$\left( \begin{array}{ccc@{\ }r} 3 & -8 & 6 & -13\\ 0 & 2 & 1 & -4\\ 2 & 3 & -1 & -7\\ \end{array} \right) \sim \ldots \sim \left( \begin{array}{ccc@{\ }r} 1 &-11 & 7 & -6\\ 0 & 2 & 1 & -4\\ 0 & 0 & 1 & -2\\ \end{array} \right)$

Nemusis ( ale mozes) pokracovat po diagonalizaciu.
Ak prepises posledny zapis ako trojuholnikovy system okamzite dostanes cakane riesenie.

janca361 · 16. 11. 2014 23:34

↑ misaH:
Ano. Už to vychází

A teď k tomu samostatnému uvěření. "Podľa mňa stačí lineárna nezávislosť 3 vektorov v 3D." - Tomu asi moc nerozumím.

misaH · 16. 11. 2014 23:38

↑ janca361:

Podľa mňa v trojrozmernom priestore bázu tvoria ľubovoľné 3 nezávislé vektory.

janca361 · 16. 11. 2014 23:44

↑ misaH:
Pokud to tak je, tak je to přesně to co píšu ↑ tady dole:.

vanok · 17. 11. 2014 01:37

Male citanie
http://en.m.wikipedia.org/wiki/Linear_combination

Matematické Fórum

#1 16. 11. 2014 22:15

Rozhodněte zda vektory tvoří bázi

#2 16. 11. 2014 22:33 — Editoval misaH (16. 11. 2014 22:45)

Re: Rozhodněte zda vektory tvoří bázi

#3 16. 11. 2014 22:50 — Editoval janca361 (16. 11. 2014 22:52)

Re: Rozhodněte zda vektory tvoří bázi

#4 16. 11. 2014 22:59 — Editoval misaH (16. 11. 2014 23:04)

Re: Rozhodněte zda vektory tvoří bázi

#5 16. 11. 2014 23:12

Re: Rozhodněte zda vektory tvoří bázi

#6 16. 11. 2014 23:16

Re: Rozhodněte zda vektory tvoří bázi

#7 16. 11. 2014 23:29

Re: Rozhodněte zda vektory tvoří bázi

#8 16. 11. 2014 23:34

Re: Rozhodněte zda vektory tvoří bázi

#9 16. 11. 2014 23:38

Re: Rozhodněte zda vektory tvoří bázi

#10 16. 11. 2014 23:44

Re: Rozhodněte zda vektory tvoří bázi

#11 17. 11. 2014 01:37

Re: Rozhodněte zda vektory tvoří bázi

Zápatí