Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » počítání pravděpodobnosti - bayesův vzorec?
#1 17. 11. 2014 18:55
počítání pravděpodobnosti - bayesův vzorec?
Vůbec nevim jak na to. "Dva lovci současně vystřelili na zajíce. Je známo, že pravděpodobnost zásahu je u prvního lovce 0,2, u druhého lovce je 0,6. Po tomto prvním výstřelu byl zajíc zasažen jednou ranou. S jakou pravděpodobností se minul první lovec? Výsledek uveďte na 5 desetinných míst".
Moje řešení zatím: P(B1)= 0,8 P(A/B1)= 0,48
P(B2)= 0,4 P(A/B2)= 0,08
Bayesův vzorec a výsledek 0,92308.
Ale přijde mi to stašně přítažený za vlasy a doufám, že se najde někdo kdo se v tom orientuje a poradími.
Offline
#2 17. 11. 2014 20:04
Re: počítání pravděpodobnosti - bayesův vzorec?
↑ Prochy75:
Dobrý den.
Řekl bych, že
jev A - trefí A, P(A) = 0.2
jev B - trefí B, P(B) = 0.6
jev C - jeden zásah zajíce
Z Bayesova vzorce plyne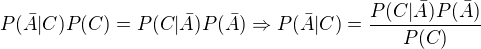
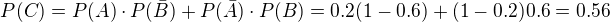
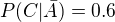
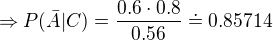
Pokud se tedy nemýlím.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » počítání pravděpodobnosti - bayesův vzorec?
