Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 04. 2009 15:21
- Cuddlesome
- Příspěvky: 76
- Reputace: 0
Odchylka přímky
Vypočtěte odchylku přímky AB a osy x, jestliže A = [2, 0], B = [4, -2].
Offline
#2 16. 04. 2009 15:34 — Editoval marnes (16. 04. 2009 15:36)
- marnes

- Příspěvky: 11227
Re: Odchylka přímky
↑ Cuddlesome:
1) Osa x má směrový vektor (1;0)
2) Přímka má směrový vektor(1;-1) a dosadíš do vzorce pro úhel
Jo. A na začátku vás zdravím.
Offline
#3 17. 04. 2009 14:30
- Cuddlesome
- Příspěvky: 76
- Reputace: 0
Re: Odchylka přímky
↑ marnes:
A kde zjistím, že má osa směrový úhel (1;0)?
Offline
#4 17. 04. 2009 14:53 — Editoval joker (17. 04. 2009 14:59)
Re: Odchylka přímky
↑ Cuddlesome:
Ahoj Lucie! :-)
Odchylku přímky od osy x zjistíš ze směrnicového tvaru přímky y = kx + q, kde číslo k představuje směrnici přímky. ![kopírovat do textarea $A=[2;0] \nl B=[4;2] \nl u=(2;-2) \nl n=(1;1) \nl$](/mathtex/2a/2af24dcf3caaa735ca8cd76657df6c48.gif)


Offline
#5 17. 04. 2009 14:59
- Cuddlesome
- Příspěvky: 76
- Reputace: 0
Re: Odchylka přímky
Aha, díky moc za vysvětlení, konečně jsem to pochopila :-)
Offline
#6 17. 04. 2009 15:01
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Odchylka přímky
↑ joker:
Možná by stálo za to vysvětlit, jak jsi došel k 45 stupňům. Směrnice přímky totiž udává tangentu úhlu, který přímka svírá s kladnou poloosou x. Zatímco odchylka dvou přímek je ten úhel ostrý (když nejsou kolmé). Takže sice arctg(-1) = 3/4 pi rad, ale nás zajímá ta zbylá čtvrtina pí, která dá 45 stupňů.
To jen pro upřesnění.
Offline
#7 17. 04. 2009 15:09
Re: Odchylka přímky
↑ halogan:
Děkuji za doplnění, já jsem se nad tím ani takhle nezamyslel. Prostě jsem bral, že když není uvedéno, který úhel z těch dvou chtějí (tedy s kterou částí osy x), tak použiju úhel ostrý.
Offline
#9 17. 04. 2009 19:51 — Editoval marnes (17. 04. 2009 19:58)
- marnes

- Příspěvky: 11227
Re: Odchylka přímky
↑ joker:
Třeba tím, že si zvolím dva body na ose x, třeba 0;0 a 1;0 a směrový vektor vznikne odečtením souřadnic, tj (1;0)
Ale i ten tvůj způsob je OK
/u.v/
Jinak při výpočtu úhlu mezi přímkami, jak bylo psáno, je to úhle vždy ostrý, takže při použití cos a=------------------
/u/./v/
hodnotu ostrou zajistí právě ta absolutní hodnota skalárního součinu v čitateli
Jo. A na začátku vás zdravím.
Offline
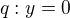 z toho zjistím normálový vektor
z toho zjistím normálový vektor 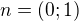 a z něho pak směrový
a z něho pak směrový 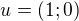 ?
?