Matematické Fórum

jardasmid · 16. 04. 2009 18:43

Já už jsem z toho jelen. snažím se vyřešit tuto separovatelnou diferenciální rovnici:
$x'=\frac{-t}{x}$
a) x(1) = 1
b) x(4) = -3

Dopracoval jsem se k tomuto, ale nevím, jestli je to dobře a za druhé si nevím rady s tím integrálem vlevo.

$h(x)=\frac{1}{x}$
$g(t) = -t$
$\int{x'(t)x(t) dt} = -\int{tdt}$

Alesak · 16. 04. 2009 18:59

Ahoj,
jednoducha pomucka pro separovatelny diferencialni rovnice je takovadle:

$x'=\frac{-t}{x}$

to se rovna

$\frac{dx}{dt}=\frac{-t}{x}$

$x\frac{dx}{dt}=-t$

ted to jakoby vynasobis, je to spis aby se to lip pamatovalo

$x dx=-t dt$

a hodis na obe strany integral, s tim ze dx a dt uz tam mas

$\int x dx=-\int t dt$

dal uz to urcite zvladnes

jardasmid · 16. 04. 2009 19:07

Aha. Jsem to dělal podle příkladu, co jsem měl v sešitě ze cvičení a tam to značí fakt nějak divně. Z tohodle to chápu. Díky moc.

jardasmid · 16. 04. 2009 19:22

Hmm, tak asi nechápu. Ve výsledku mají napsáno toto:
Obecné řešení $x(t)=\sqrt{c^2-t^2}$ , $x(t)=-\sqrt{c^2 - t^2}, t\in(-c,c)$ pro c>0

a) $x(t)=\sqrt{2 - t^2}, t\in(-\sqrt{2},\sqrt{2})$
b) $x(t)=-\sqrt{25 - t^2}, t\in(-5,5)$

A z toho, co jsi napsal, dostanu
$\frac{x^2}{2} = -\frac{t^2}{2} + c$
$x = \sqrt{2c - t^2}$

jardasmid · 16. 04. 2009 19:35

Už to vidím, ono je asi jedno, kolikrát nebo nakolikátou to c je, ono to vyjde.

Alesak · 16. 04. 2009 19:40

$\frac{x^2}{2} = -\frac{t^2}{2} + c$ je spravne. ted pridou dva triky:

po vynasobeni dvema dostaneme

$x^2 = -t^2{2} + 2C$

a ted trik je napsat misto 2C jenom C, potom az budes dosazovat pocatecni podminky tak se to C samo zmeni a vysledek bude spravne. takze misto C^2, C + 350, e^C, proste cokoliv kde to bude porad neznama konstanta, muzes napsat proste C a ono se to potom samo opravi. nemuzes ale udelat treba z C*x jenom C.

$x^2 = -t^2{2} + C$

druhej trik je v odmocnine, reseni treba x^2 = 4 je +- dva, takze i tady to bude

$x = \pm \sqrt{-t^2 + C}$

to se shoduje s tim resenim co uvadi oni.

kaja.marik

$x = \pm\sqrt{2c - t^2}$

udelam substituci 2c=A a dostanu

$x = \pm\sqrt{A - t^2}$

a protoze pro A zaporne by takova funkce nebyla nikde definovana muzu (napriklad z perverznich pohnutek) misto A psat druhou mocninu konstanty C. Tim dostanu
$x(t)=\sqrt{C^2-t^2}$ a $x(t)=-\sqrt{C^2 - t^2}, t\in(-C,C)$

pismenko kterym oznacuju konstantu nehraje roli.

----------------
jo tak to tohle mezitimnapsal i kolega prede mnou tak jenom zakoncim, ze pokud se v integralu
$\int{x'(t)x(t) dt} = -\int{tdt}$
udela substituce x=x(t), dx=x'(t)dt tak dostanu
$\int x dx=-\int t dt$

Takze postup v sesite a postup od Alesaka jsou jine zapisy tehoz.

Alesak · 16. 04. 2009 19:50

↑ kaja.marik:

mam dotaz, myslim si spravne ze kdyz tam nasobim celou rovnici dt, ze je to spatne?

dx/dt je podle me akorat operator d/dt pouzitej na x, a je to akorat forma zapisu kde je nahodou zlomek. na druhou stranu derivace je podil dx ku dt, takze kdyz se spokojim s tim ze budu mit nekonecne maly cisla nekde od sebe tak by to melo bejt ok.

jardasmid · 16. 04. 2009 20:03

Nějak mi nejde do hlavy to mínus. Chápu to plus/mínus před odmocninou, ale né to "pouze plus" a "pouze mínus". Ve výsledku je pro x(4) = -3 uvedeno řešení
$x(t) = -\sqrt{25-t^2}$
Ale já bych chápal $x(t) = \pm\sqrt{25-t^2}$

kaja.marik · 16. 04. 2009 20:04

↑ Alesak:
Zdravim.

dx/dt opravdu neni zlomek takze nasobit dt je opravdu nesmysl. Ale dela to tak kazdy :) Jak je to mozne?

Kdyz se k tomu chovame dx/dt jako k operatoru, postupujeme opatrne a potom udelame tu substituci, o ktere pisu vyse, tak to stejne potom opticky jako vynasobeni dt a zintegrovani vypada.

Takze nekdy treba rikam tohle: Da se dokazat (a dukazy preskakujeme, takze mi musite verit), ze i kdyz dx/dt neni podil, tak tohle je jeden z mala pripadu kdy se k tomu formalne jako k podilu muzeme chovat a postupujeme tak, ze .........

kaja.marik · 16. 04. 2009 20:05

↑ jardasmid:
odmocnina je kladna, minus odmocnina zaporna.
pocatecni podminka jednoznacne rika jestli mam vybrat plus nebo minus, podle toho, jestli se to ma rovnat kladnemu (pripad a) nebo zapornemu cislu (pripad b)

jardasmid · 16. 04. 2009 20:08

↑ jardasmid: Aha, mám vlastně dostat -3, tak tam musí být mínus, už to chápu. Tak všem moc děkuju. Neloučím se ale na dlouho, asi se ještě ozvu kvůli lineárním diferenciálním rovnicím s konst koeficienty :-)

Alesak · 16. 04. 2009 20:14

↑ kaja.marik:

no, kdyz bereme dx/dt jako operator, tak to nasobit nejde, jenze kdyz to vezmeme podle definice ze derivace je zmena x ku zmena t, tak by davalo smysl ze to je zlomek a melo by to jit vynasobit. tady bych videl problem v tom ze kdyz to je v podilu, tak dostaneme normalni cislo, zatimco kdyz si dt odnasobime nekam pryc tak se nam po rovnici poflakujou dve nekonecne maly cisla, coz neni dobry.

Alesak · 16. 04. 2009 20:15

↑ jardasmid:↑ jardasmid:

jestli ti nevadi anglictina tak doporucuju tenhle tutorial, je super.

kaja.marik · 16. 04. 2009 20:34

Alesak napsal(a):
↑ kaja.marik:

... jenze kdyz to vezmeme podle definice ze derivace je zmena x ku zmena t.....

to je takova hodne volne recena definice. V presne definici derivace neni podil ale limita podilu.

jardasmid · 16. 04. 2009 20:57

↑ Alesak:Nevadí, díky.

jardasmid · 16. 04. 2009 22:14

Ještě dotaz, tohle asi není správně?

$x' = \frac{1-x^2}{2tx}$
$\frac{dx}{dt} = \frac{1-x^2}{x}\frac{1}{2t}$
$\int{\frac{x}{1-x^2}}dx=\int{\frac{1}{2t}}dt$
$\int{\frac{x}{(1-x)(1+x)}dx}=\frac{1}{2}ln(t)+\frac{1}{2}ln(c)$
$\frac{1}{2}\int{\frac{1}{1-x}dx} - \frac{1}{2}\int{\frac{1}{1+x}dx} = \frac{1}{2}ln(Ct)$
$\frac{1}{2}ln\frac{1-x}{1+x} = \frac{1}{2}ln(Ct)$
$\frac{1-x}{1+x} = Ct$
$x=\frac{1-Ct}{1+Ct}$

Když ve výsledku je
$x(t) = \pm\sqrt{1-\frac{c}{t}}$

kaja.marik · 16. 04. 2009 22:27

ten integral parcialnich zlomku vypada spatne

zkuste radeji subtituci 1-x^2=s

jardasmid · 16. 04. 2009 22:43

↑ kaja.marik:
Jejda, špatný znaménko :-)

Rumburak

↑ kaja.marik:, ↑ Alesak:
Zdravím, kolegové. Dovolím si připojit několik poznámek k vaší diskusi o symbolech dx, dy a jejich vztahu k derivacím.
Je-li f funkce mající v bodě c vlastní derivaci f'(c), pak symbol df(c) značí diferenciál fce f v bodě c, tj. lineární formu $L_{f,c}$
(přiřazenou fci f a bodu c), pro niž je splněna rovnice
$\lim_{h \to \0}\frac{f(c+h)-f(c)-L_{f,c} (h)}{h}=0$ .
Není těžké ukázat, že pak
(1) $L_{f,c} (h)\equiv f'(c)\,h$
(tímto zápisem míním, že rovnice je splněna "pro každé h").
Při pevném f tedy symbol df značí zobrazení, které bodu c přiřadí lin. formu $L_{f,c}$ . Píšeme-li y = f(x), pak je licencováno psát dy místo df.
Pro identitu y = x (= f(x)) je dokonce licencováno psát dx místo df.
Dále: je-li f identita, potom f'(c)= 1 a tedy $L_{id,c} (h)\equiv h$ , což je možno pomocí výše uvedených licencí psát jako $dx(h)\equiv h$ ,
zpětně pak rovnici (1) pro obecné f napíšeme ve tvaru
(2) $L_{f,c} (h)\equiv f'(c)\,dx(h)$ .
Její levou stranu rovněž licenčně upravíme :
(3) $L_{f,c} (h)\equiv df(c,h)\equiv dy(c,h)$ .
Spojením (2) a (3) získáme $dy(c,h)\equiv f'(c)\,dx(h)$ a odhlédnutím od c, h $dy= f'dx$ .
Dalšími kroky pak mohou být nahrazení symbolu 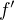$f'$ symbolem 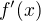$f'(x)$ a "vydělení" výrazem dx.
Z rigorosního hlediska je to sice serie prasáren, ale dobře se s tím provádějí mnohé výpočty.

Alesak · 17. 04. 2009 22:22

↑ Rumburak:

takhle napsano jsem to jeste nevidel, budu si muset zjistit co to je linearni forma...

Rumburak

↑ Alesak:
Lineární forma definovaná na lineárním prostoru W nad tělesem R je funkce f : W ----> R , která vyhovuje rovnicím

f(x + y) = f(x) + f(y) , f(r*x) = r*f(x)

pro libovolná x, y element W , r element R. Je to vlastně lineérní zobrazení (neboli homomorfismus) z lin. prostoru W
do lin. prostoru R. Těleso R lze chápat jako lineární prostor nad sebou samým.

PS. 1. Lineárními formami na lin. prostoru R všech reálných čísel jsou právě všechny funkce f : R ----> R tvaru

f(x) = k*x pro každé x,

kde k je konstanta.
2. Z praktického pohledu pojem diferenciálu funkce jedné proměnné splývá s pojmem vlastní derivace (fce jedné proměnné má v bodě diferenciál
právě tehdy, má-li v něm vl. derivaci , přičemž ta hraje roli konstanty k ve výrazu k*h pro diferenciál.) Význam diferenciálu se projeví až
u funkcí více proměnných, kde je situace značně složitější.

Matematické Fórum

#1 16. 04. 2009 18:43

Diferenciální rovnice (separovatelná)

#2 16. 04. 2009 18:59

Re: Diferenciální rovnice (separovatelná)

#3 16. 04. 2009 19:07

Re: Diferenciální rovnice (separovatelná)

#4 16. 04. 2009 19:22

Re: Diferenciální rovnice (separovatelná)

#5 16. 04. 2009 19:35

Re: Diferenciální rovnice (separovatelná)

#6 16. 04. 2009 19:40

Re: Diferenciální rovnice (separovatelná)

#7 16. 04. 2009 19:43 — Editoval kaja.marik (16. 04. 2009 19:45)

Re: Diferenciální rovnice (separovatelná)

#8 16. 04. 2009 19:50

Re: Diferenciální rovnice (separovatelná)

#9 16. 04. 2009 20:03

Re: Diferenciální rovnice (separovatelná)

#10 16. 04. 2009 20:04

Re: Diferenciální rovnice (separovatelná)

#11 16. 04. 2009 20:05

Re: Diferenciální rovnice (separovatelná)

#12 16. 04. 2009 20:08

Re: Diferenciální rovnice (separovatelná)

#13 16. 04. 2009 20:14

Re: Diferenciální rovnice (separovatelná)

#14 16. 04. 2009 20:15

Re: Diferenciální rovnice (separovatelná)

#15 16. 04. 2009 20:34

Re: Diferenciální rovnice (separovatelná)

Alesak napsal(a):

#16 16. 04. 2009 20:57

Re: Diferenciální rovnice (separovatelná)

#17 16. 04. 2009 22:14

Re: Diferenciální rovnice (separovatelná)

#18 16. 04. 2009 22:27

Re: Diferenciální rovnice (separovatelná)

#19 16. 04. 2009 22:43

Re: Diferenciální rovnice (separovatelná)

#20 17. 04. 2009 11:07 — Editoval Rumburak (17. 04. 2009 14:49)

Re: Diferenciální rovnice (separovatelná)

#21 17. 04. 2009 22:22

Re: Diferenciální rovnice (separovatelná)

#22 20. 04. 2009 08:38 — Editoval Rumburak (20. 04. 2009 10:37)

Re: Diferenciální rovnice (separovatelná)

Zápatí