Matematické Fórum

↑ Callme:
Mám dojem, že taková tečna neexistuje.
Máš dobře zadání úlohy?

Zdravím,

↑ Callme:
pokud je zadání dobře, tak můžeš začít řešit, jak navrhuješ

Po 1. urcim smernicu priamky?

se rozumí pro přímku . S čím to máš v plánu porovnat (nebo jinak využit)? Pokud bude problém v zadání, tak to nejspíš poznáme, že narazíme na některou potíž (zatím se nenarazilo).

↑ Callme:

můžeš tomu říkat graf lineární funkce (a v pojmu "směrnice", že využíváš geometrický smysl derivace). Nevyužitím analytické geometrie se spíš rozumí, že nepojdeš rovnou pro vzorce tečny k hyperbole (jak se bere v analytické geometrii na SŠ), ale že máš před sebou implicitně zadanou funkci a sestrojuješ tečnu takové funkce.

↑ Callme:
Ne.
Pokud má být tečna kolmá na přímku , směrnice tečny bude
Nyní derivací podle rovnice hyperboly dostaneš
z čehož vyjádříš
V bodě dotyku musí být
Tak dostáváš soustavu dvou rovnic (protože bod dotyku leží na hyperbole)

Řešením této soustavy snadno zjistíš (jak už psal ↑ Cheop:), že bod dotyku neexistuje.

Zdravím,

Callme napsal(a):

Dosadim do
?

Když vezmeš předpis pro přímku a dosadíš do rovnice kuželosečky a tuto rovnici vyřešíš, tak jaké možné výsledky takových řešení můžeš mít a co každé takové řešení znamená? Tento dotaz skoro nesouvisí s úlohou, spíš s pokusem přimět, abys viděl, že tento návrh se zadáním nic společného nemá, ale nějaký výsledek by Tobě z toho vyšel a mylně bys ho považoval za použitelný.

K problému:

Úloha požaduje, abys hledal přímku, která je kolmá k zadané . Jakou vlastnost budou mít směrnice takových přímek?

Riesenim sustavy mozu byt komplexne korene?

to mohou, ale hned na úvod jsi napsal, že  "Mam pouzit diferenciálny pocet reálnej funkcie jednej reálnej premennej". 

Bod dotyku neexistuje preto lebo dosadenim...

viz začátek tohoto mého příspěvku - dosazováním jdeš úplně jinam. Rozmyslí si úlohu, nakresli si náčrt (nic podrobného), jak by to vypadalo, že zadána přímka, hyperbola a hyperbola má tečnu přímce kolmou.

Kedze nema dotycnicu takze nema ani rovnicu dotycnice?

:-) to je až filosofická otázka - co neměla dřív?

↑ Callme:

děkuji. To bys pravě potřeboval si uvědomit, že pokud řešíš soustavu rovnic

(Tvé dosazování), tak ve skutečnosti vyšetřuješ vzájemnou polohu zadané kuželosečky a zadané přímky a mohou být situace: žádný společný bod, jeden společná bod, 2 společné body (jak bude vypadat řešení soustavy v těchto případech?). Tedy bys z tohoto kroku nějaký výsledek dostal, ale zcela nepoužitelný pro Tvé zadání.

Zde zadaná přímka je pouze pomocná a udává vlastnost přímky, která má být tečnou. Tedy ze zadané přímky vytáhneš pouze dle vlastností a

a tu smernicu zistim ako? ?

Ano, tak máš směrnici hledané nové přímky - tečny. Dál už kolega Zdeněk ↑ příspěvek 8: (už bys neměl mít nejasno), nebo se ještě zeptej, prosím.

To co riesim skor

no vidíš :-)

↑ Callme:

Tobě by se hodilo držet se některého studijního materiálu alespoň pro některý souvislý úsek látky - nejlépe pro celý kurz. Co používáš?

Jelikož takhle jsi na fórech posbíráš nějaká moudra, co plynou z určité zkušenosti/zvyku odpovídajících, ale netvoříš si tím sobě žádnou použitelnou teoretickou a praktickou bázi.

funkce po přepisu je implicitně zadána funkce . Odkaz -  buď počítáš podle věty 5.3.2 s využitím parciálních derivací nebo podle Poznámky hned za větou, jako kolega ↑ zdenek1: (že 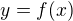a část se derivuje jako složená funkce). Kterou metodu jsi tedy použil? Děkuji.

↑ Callme:

pokud se tím myslí, že , tak ano.

Co tym myslis? Pouzivam len to co najdem na internete

Tím myslím, že předmět, který studuješ, má studijní plán a doporučenou literaturu. Pokud to jsou knihy a jiné materiály pro Tebe nedosažitelné, tak si vyhledat na internetu některý shodný souborný materiál, který cca tomu vašemu odpovídá. Např. podle typu školy, nebo podle jiného vhodného hlediska. Z osvědčeného zdroje, s jasným autorem a s návaznosti jednotlivých kapitol - např. materiály VŠB. Stránku předmětu máte online? Děkuji.

↑ Callme:

v knize nemusí být přesný popis - návod. Pravděpodobně v ni najdeš "geometrický význam derivace" a souvislost mezi derivaci v bodě a tečnou ke křivce.

Potom k úloze máš přistupovat tak: "Nájdite dotycnicu k hyperbole" (Mam pouzit diferenciálny pocet reálnej funkcie jednej reálnej premennej bez pouzitia analytickej geometrie.) To je pro Tebe návěst k to, co se požaduje a jakou metodou.

V geometrickém významu derivace bys měl mít zadán bod dotyku, ve kterém tečnu sestrojuješ. Místo toho zde máš zadanou přímku, o které víš, že s tečnou kolmá. Tedy svou úlohu pozměníš - představuješ, že rovnici tečny již máš a z pomocné přímky jsi odvodil směrnici tečny. Nakonec použiješ fakt, že tečná přímka má s kuželosečkou jeden společný bod a jeho souřadnice lze najít vyřešením soustavy rovnic ( kolegy ↑ zdenek1:

Soustava říká, že bod leží zároveň na tečně a na hyperbole. Pokud jsi takový bod nenašel (soustava řešení nemá), potom není možné sestrojit tečnu dle požadavku úlohy.

To jen chci ukázat, že první

Callme v 1. příspěvku napsal(a):

Po 1. urcim smernicu priamky?

Tobě zůstane "viset ve vzduchu", protože jsi před tím neprovedl rozbor, na co takovou směrnici potřebuješ.

V knize hledej podstaty metod (teoretické odůvodnění, předpoklady), ne konkrétní návody na každou maličkost. Kniha se nějak jmenuje? Děkuj.

↑ Callme:

děkuji, nedával jsi mi již odkaz na tuto knihu?

Myslím, že je dostačující - má velké povídání o kuželosečkách (kde si se dočteš o vlastnostech křivek jako funkcí), potom je kapitola 4.1, kde podrobně o geometrickém významu derivace a použití pro tečny a normály, na závěr jsou případy derivování funkcí zadaných implicitně a parametricky - to, myslím, dává komplexní pohled na problém. (rozumím, že mám načteno o trošku více, tedy cca vím, kde co hledat).

Tak jsi také materiál četl i včetně všech teoretických výkladů a vyřešených příkladů, nebo vyloženě hledáš Tvůj typ úlohy? Děkuji.

↑ Rumburak:

Zdravím a děkuji, jen k

2. Bylo by užitečné využívat nejen internet, ale také studijní materiály doporučené přednášejícím (učebnice, skripta).

kolega přidal odkaz na jejich materiál v ↑ příspěvku 19:, ten jsem zběžně rozebrala. Jelikož ještě nemají funkce více proměnných, tak parciální derivace pro použití u implicitních funkcí zavádějí celkem opatrně a jen k "technickému použití" (skoro na závěr textu). A spíš to berou ještě jako funkci jedné proměnné (poznámka 4.3.30 se složenou funkci jedné proměnné x).

1.  Má-li být použit diferenciální počet funkcí pouze jedné proměné , pak vyjádříme rovnici hyperboly (resp. její části)
ve tvaru funkce jedné proměnné a použijeme větu o geometrickém významu derivace.

to mám obavu, že kolegu trochu poděsíš :-) Může, prosím, zůstat u implicitních funkcí (viz příspěvek kolegy Zdeňka)? Děkuji.

jelena napsal(a):

↑ Callme:děkuji, nedával jsi mi již odkaz na tuto knihu?

Ja nie.

jelena napsal(a):

Tak jsi také materiál četl i včetně všech teoretických výkladů a vyřešených příkladů, nebo vyloženě hledáš Tvůj typ úlohy? Děkuji.

Tu knihu som takmer nepouzil. Vyuzival som len to co som nasiel na internete lenze z toho co som nasiel tak som to ja nedokazal vyriesit.