Matematické Fórum

Callme · 25. 11. 2014 23:32 — Editoval Callme (25. 11. 2014 23:37)

Cavte ako urcim polynom
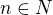Urcte Maclaurinov polynóm $T_{n}(x)$ stupna $n\in N$ pre funkciu $f(x) = cos x, x\in R$ .
Maclaurinov polynóm je Taylorov polynóm so stredom v x=0.
Pre stupen 5 budu Derivace, derivace v bodě 0 a koeficienty Taylorova polynomu vyzerat takto?
//forum.matweb.cz/upload3/img/2014-11/53514_mm.png
Ako urcim clen n? $T_{n}(x) =1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}+...?$

vlado_bb

↑ Callme:Podla zadania ale nemas urcit $n$ . Podla zadania je $n$ znama hodnota a treba najst $T_n$ , teda vlastne k tomu, co uz mas, treba iba zapisat clen s $n$ -tou mocninou. Pripadne si napis este dva dalsie cleny a veci budu jasnejsie.

Callme · 26. 11. 2014 12:48 — Editoval Callme (26. 11. 2014 12:57)

$T_{n}(x) =1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}+...+(-1)^{n}\frac{(x^{2n})}{(2n)!}$ ?

vanok · 26. 11. 2014 14:00 — Editoval vanok (26. 11. 2014 14:42)

Ahoj ↑ Callme:,
Porozmyslaj este trochu o tom.
Z tvojej tabulky si iste konstatoval, ze ak n= 2m je parne cislo, cislo tak $T_{2m} =T_{2m+1}$ .
Uvedom si ze ide o approximaciu ( od presnej hodnoty f(x), sa lisia ...).

vlado_bb · 26. 11. 2014 14:05

↑ vanok:Mal najst len polynom, o zvysku nebola rec.

vanok · 26. 11. 2014 14:23

↑ vlado_bb:,
Zvysok to je kulturna poznamka, aby citatel mohol dokonca le rozumiet o co ide. Tu nejde len o odpoved, ale o moznost nieco sa naucit.

vlado_bb · 26. 11. 2014 14:29

↑ vanok:No ved predpokladam, ze Callme by sa neznizil k tomu, aby pocital nieco, comu nerozumie.

Rumburak

↑ Callme:

Ahoj.

Pro $n = 0, 1, 2, 3, ...$ je n-tý člen MacLaurinova rozvoje funkce $f$ roven $\frac{f^{(n)}(0)}{n!} x^n$ .
Jde o speciální případ Taylorova rozvoje.

Callme · 26. 11. 2014 14:55

↑ Rumburak:
Tymto narazas k tomuto

Callme napsal(a):
Ako urcim clen n?

alebo ze mam zly vysledok?

vanok · 26. 11. 2014 15:06 — Editoval vanok (26. 11. 2014 15:30)

↑ Callme:,
Poznamka len k tvojmu cviceniu.
Ak si cital co som napisal,vies, ze n je dane,
ty musis vediet co je parne alebo nie.
A pouzit potom to co som vyssie napisal.
Pozor, i ked si to trochu opravil ↑ Callme:, nie je to presne
Mohol si to upravit napr takto
$T_{n}(x) =1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}+...+(-1)^{m}\frac{(x^{2m})}{(2m)!}$ , ak n= 2m alebo n= 2m+1.

Dobre pokracovanie.

Callme · 26. 11. 2014 15:37 — Editoval Callme (26. 11. 2014 15:39)

↑ vanok:
Preco to nie je presne nebude to obsahovat vsetky cleny?

vanok · 26. 11. 2014 15:50

Lebo v pripade neparneho n, posledny clen je nulovy.to je presne pricina, ze sa tu moze pisat ↑ vanok:
Staci?

Rumburak · 26. 11. 2014 16:50

↑ Callme:

Ano, na tento dotaz jsem reagoval.

Chybu máš v tom, že toto $1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}+...+(-1)^{n}\frac{(x^{2n})}{(2n)!}$
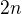je MacL. polynom funkce $x \mapsto \cos x$ stupně $2n$ a nikoliv $n$ .

Máme-li tedy být algebraicky korektní, musíme říci, že uvažovaná funkce má MacL. polynomy pouze sudých stupňů.

vanok · 26. 11. 2014 18:04 — Editoval vanok (26. 11. 2014 18:06)

Pozdravujem ↑ Rumburak:,
Ano chyba sa da vidiet z tej strany ( ktory v tom pripade nie je vseobecny, lebo zabuda neparne pripady), alebo v poslednom clene, ako som to vyssie napisal ( v neparnom pripade, posledny clen rozvoja je 0).

Najdolezitejsie je rozumiet dobremu vysledku ( vo vseobecnom pripade).

Callme · 26. 11. 2014 19:14 — Editoval Callme (26. 11. 2014 19:30)

Cize nemoze to vyzerat takto $T_{n}(x) =1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}+...+(-1)^{n}\frac{(x^{2n})}{(2n)!}$ lebo nech dosadim za n lubovolne cislo z N tak stale bude vychadzat vysledok len pre parny stupen a nie pre neparny? Ja som najprv skusal $\frac{x^{n}}{n!}$ lenze tu to neviem upravit tak aby pre 2.,6.,10. ... stupen bol vysledok zaporny alebo ako inak bude vyzerat $(-1)^{n}\frac{(x^{2n})}{(2n)!}$ aby to vyhovovalo parnym aj nepanym stupnom?

vanok · 26. 11. 2014 19:38

↑ Callme:,
Vsak to je ta chyba o ktorej som pisal, ↑ vanok:, to som tam vysvetlil.

vanok · 26. 11. 2014 19:41

Priklady $T_{2}(x)=T_{3}(x) =1-\frac{x^{2}}{2!}$
$T_{4}(x) =T_{5}(x)=1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}$

Callme · 26. 11. 2014 22:13

↑ vanok:
No to je pravda a co s tym?

vanok · 26. 11. 2014 22:17

No to je odpoved na tvoje cvicenie.

vlado_bb · 26. 11. 2014 22:18

↑ Callme:Co by s tym malo byt? Je to tak ako pise vanok, $T_{2n+1}=T_{2n}$ .

vanok · 26. 11. 2014 22:24

↑ vlado_bb:
Pis skor $T_{2m} =T_{2m+1}$ , ako ↑ vanok:. To preto aby bol respektovany text cvicenia.

Callme · 26. 11. 2014 22:44 — Editoval Callme (26. 11. 2014 22:48)

To akoze napisem len toto $T_{2m} =T_{2m+1}$ a z toho je vidiet riesenie ?
Ked napisem toto $T_{2m} =T_{2m+1}=1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}+...+(-1)^{m}\frac{(x^{2m})}{(2m)!}$ tak to je chyba?

vlado_bb · 26. 11. 2014 22:47

↑ Callme:Nie, riesenim je odpoved na otazku z tvojho prveho prispevku. A ta uz v tejto diskusii je, treba len citat a rozmyslat.

Callme · 26. 11. 2014 23:02 — Editoval Callme (26. 11. 2014 23:09)

↑ vlado_bb:
Naco som potom toto $T_{2m} =T_{2m+1}$ riesil k comu je to dobre aby som ukazal ze polynom nejakeho stupna je rovnaky ako polynom stupna o 1 väcsieho lebo obsahuje 0?
Cize vysledkom je $T_{n}(x) =1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}+...+(-1)^{m}\frac{(x^{2m})}{(2m)!}$ a toto $T_{2m} =T_{2m+1}$ je len obycajna podmienka?

vlado_bb · 27. 11. 2014 09:51

↑ Callme:Nie. Otazka znie, ako vyzera polynom stupna $n$ , takze aj v odpovedi by sa to $n$ malo vyskytovat.

Matematické Fórum

#1 25. 11. 2014 23:32 — Editoval Callme (25. 11. 2014 23:37)

Maclaurinov polynóm

#2 26. 11. 2014 04:49 — Editoval vlado_bb (26. 11. 2014 04:52)

Re: Maclaurinov polynóm

#3 26. 11. 2014 12:48 — Editoval Callme (26. 11. 2014 12:57)

Re: Maclaurinov polynóm

#4 26. 11. 2014 14:00 — Editoval vanok (26. 11. 2014 14:42)

Re: Maclaurinov polynóm

#5 26. 11. 2014 14:05

Re: Maclaurinov polynóm

#6 26. 11. 2014 14:23

Re: Maclaurinov polynóm

#7 26. 11. 2014 14:29

Re: Maclaurinov polynóm

#8 26. 11. 2014 14:34 — Editoval Rumburak (26. 11. 2014 14:36)

Re: Maclaurinov polynóm

#9 26. 11. 2014 14:55

Re: Maclaurinov polynóm

Callme napsal(a):

#10 26. 11. 2014 15:06 — Editoval vanok (26. 11. 2014 15:30)

Re: Maclaurinov polynóm

#11 26. 11. 2014 15:37 — Editoval Callme (26. 11. 2014 15:39)

Re: Maclaurinov polynóm

#12 26. 11. 2014 15:50

Re: Maclaurinov polynóm

#13 26. 11. 2014 16:50

Re: Maclaurinov polynóm

#14 26. 11. 2014 18:04 — Editoval vanok (26. 11. 2014 18:06)

Re: Maclaurinov polynóm

#15 26. 11. 2014 19:14 — Editoval Callme (26. 11. 2014 19:30)

Re: Maclaurinov polynóm

#16 26. 11. 2014 19:38

Re: Maclaurinov polynóm

#17 26. 11. 2014 19:41

Re: Maclaurinov polynóm

#18 26. 11. 2014 22:13

Re: Maclaurinov polynóm

#19 26. 11. 2014 22:17

Re: Maclaurinov polynóm

#20 26. 11. 2014 22:18

Re: Maclaurinov polynóm

#21 26. 11. 2014 22:24

Re: Maclaurinov polynóm

#22 26. 11. 2014 22:44 — Editoval Callme (26. 11. 2014 22:48)

Re: Maclaurinov polynóm

#23 26. 11. 2014 22:47

Re: Maclaurinov polynóm

#24 26. 11. 2014 23:02 — Editoval Callme (26. 11. 2014 23:09)

Re: Maclaurinov polynóm

#25 27. 11. 2014 09:51

Re: Maclaurinov polynóm

Zápatí