Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 11. 2014 21:23
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
tečny od Janca96
rozděleno z tématu
vlado_bb napsal(a):
↑↑ Janca96:K dotycniciam: dotycnica je priamka, teda jej predpis je
. Ak ide o dotycnicu k funkcii
v bode
a existuje vlastna (teda realna) derivacia v tomto bode, tak
. No a
dopocitas z toho, ze poznas jeden bod dotycnice, konkretne bod
.
Offline
- (téma jako nevyřešené označil(a) jelena)
#3 28. 11. 2014 13:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: tečny od Janca96
↑ Cheop:
Zdravím,
došel mi mail (přes službu fóra), že jsi vyřešil můj problém (čas mailu 10:13, příspěvek 8:27) - to jsou mi služby :-) Jen aby autorka původního problému nebyla trochu zmatená - při zadání 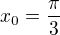 bod dotyku není zaokrouhleně (a následně ani
bod dotyku není zaokrouhleně (a následně ani  v rovnici tečny), ale
v rovnici tečny), ale ![kopírovat do textarea $[\frac{\pi}{3},f(\frac{\pi}{3})]$](/mathtex/ed/eda53dd60609398bef14a6750e83f8ea.gif) .
.
Děkuji, jiné problémy momentálně nemám (zaklepu velmi), na poštu pro kolek potřebuji, ale to snad cestou zvládnu.
Offline
#5 28. 11. 2014 21:34
Re: tečny od Janca96
↑ Janca96:Cisla na obrazku pri 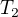 si nevsimaj, su priblizne a urcite by ti neboli uznane ako spravne riesenie. Ak chces vediet suradnice bodu dotyku, tak prvu suradnicu mas danu v texte ulohy, teda
si nevsimaj, su priblizne a urcite by ti neboli uznane ako spravne riesenie. Ak chces vediet suradnice bodu dotyku, tak prvu suradnicu mas danu v texte ulohy, teda 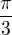 no a druhu si uz lahko dopocitas, pretoze ide o bod leziaci na grafe funkcie
no a druhu si uz lahko dopocitas, pretoze ide o bod leziaci na grafe funkcie 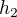 . Staci takto? A ostatnych prosim, aby dovolili Janca96 rozmyslat a dalej ju posunuli az potom, ako ona sama napise, ze toto vysvetlenie jej nestaci a zdovodni, comu v nom nerozumie.
. Staci takto? A ostatnych prosim, aby dovolili Janca96 rozmyslat a dalej ju posunuli az potom, ako ona sama napise, ze toto vysvetlenie jej nestaci a zdovodni, comu v nom nerozumie.
Offline




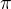 ? a výslednpu rovnici pomocí
? a výslednpu rovnici pomocí