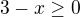Matematické Fórum

k.niccy@seznam.cz · 19. 04. 2009 12:01

Ahoj prosím o pomoc s touto rovnicí:

Děkuji.

k.niccy@seznam.cz · 19. 04. 2009 12:03

J to rovnice za C,to jsem zapomněla dodat:-)

matoxy · 19. 04. 2009 14:24 — Editoval matoxy (19. 04. 2009 14:33)

Ahoj!
Najskôr stanovím podmienky riešiteľnosti: a.) výraz 1-x nesmie byť záporný
b.) výraz 1+x nesmie byť záporný
Na akom intervale teda riešim rovnicu?
Rovnicu vynásobím 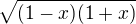$\sqrt{(1-x)(1+x)}$ .
Dostanem 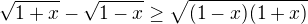$\sqrt{1+x}-\sqrt{1-x}\geq\sqrt{(1-x)(1+x)}$ . Umocním na druhú
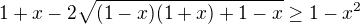$1+x-2\sqrt{(1-x)(1+x)+1-x}\geq1-x^2$ posčitujem čo viem a všetko okrem odmocniny "upracem" doprava.
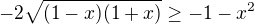$-2\sqrt{(1-x)(1+x)}\geq-1-x^2$ znova umocním na druhú.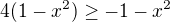
$4(1-x^2)\geq-1-x^2$
$3x^2\geq5$
$\mid x \mid\geq\sqrt{\frac53}$
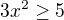
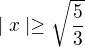
Tento výsledok zapíšeme intervalom a spravíme prienik s intervalom na ktorom rovnicu riešime.

k.niccy@seznam.cz · 19. 04. 2009 14:36

Mně to tak také vyšlo,ale dle výsledků to má vyjít takto:

(spodní výsledek)

joker · 19. 04. 2009 17:42 — Editoval joker (19. 04. 2009 19:46)

↑ matoxy:

Zdravim,

mám pocit, že jsi v tomto kroku "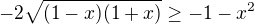 $-2\sqrt{(1-x)(1+x)}\geq-1-x^2$ znova umocním na druhú." zapomněl umocnit i druhou stranu rovnice. Takže pokračování by bylo:

$-2\sqrt{(1-x)(1+x)}\geq-1-x^2 \nl 2\sqrt{(1-x)(1+x)}\le 1+x^2 \nl 4(x^2-1)\le 1+2x^2+x^4 \nl 0\le x^4+6x^2-3$

Zde je asi nejvhodnější zavést substituci za $x^2$ a po dopočítání, zpetněm dosazení do substituce a sjednocení s podmínkami vychází skutečně $x\in <\sqrt{-3+2\sqrt{3}};1)$ .

k.niccy@seznam.cz · 19. 04. 2009 18:18

Děkuji,ted už chápu proč to tak vychází:-)

halogan · 19. 04. 2009 18:25

Jen mi přijde zvláštní, že máme obě strany očividně záporné (resp. jednu určitě, druhou u většiny x) a bez problému mocníme.

$-6 < -2 \nl 36 < 4$

Což nedává smysl.

lukaszh · 19. 04. 2009 19:09

↑ joker:

Až teraz môžeš umocniť.

halogan · 19. 04. 2009 19:12

↑ lukaszh:

No to ano, s tím souhlasím... ale to se tam (výše) neděje.

lukaszh · 19. 04. 2009 19:14

↑ halogan:
Preto to aj zle vychádza :-) ↑ joker: si trochu nechal uniknúť význam symbolu $\le$ .

joker · 19. 04. 2009 19:44

↑ lukaszh:

Omlouvám se, samozřejmě to tak je, já už neumim nic ani přepsat. Počítal jsem na papír a pak už musel jít na hokej do hospody a při přepisování do TeXu jsem to v rychlosti takhle zamotal jak idiot!

vonSternberk · 07. 05. 2009 10:21

kde jsem udělal chybu?
najděte všechna řešení iracionální rovnice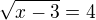
$\sqrt{x-3}=4$
$\sqrt{x-3}=4/^2$
$x-3=2$
$x=5$
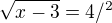
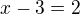
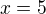
ale má vyjít x=19

Cheop · 07. 05. 2009 10:30

↑ vonSternberk: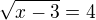
$\sqrt{x-3}=4$ umocníme tedy: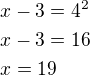
$x-3=4^2\nlx-3=16\nlx=19$
Ty jsi levou stranu rovnice umocnil, ale pravou stranu jsi odmocnil

vonSternberk · 07. 05. 2009 10:32

jj pravda...dík

vonSternberk · 10. 05. 2009 12:03

zkontrolujte mi někdo prosím toto: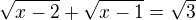
$\sqrt{x-2}+\sqrt{x-1}=\sqrt{3}$
$\sqrt{x-2}+\sqrt{x-1}=\sqrt{3}/^2$
$x-2+x+1=3$
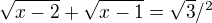
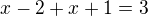
...rovnice nemá řešení
...jenomže ve výsledku je že x=7/3

O.o · 10. 05. 2009 12:12

↑ vonSternberk:

Nejčastější chyba co se dělá je, že člověk asi neumí správně pracovat s mocninami, protože (vykřičníky si dej k tomu, jak se to umocňovalo!):

$\sqrt{x-2}+\sqrt{x-1}=\sqrt{3} \nl (\sqrt{x-2}+\sqrt{x-1})^2=(\sqrt{3})^2 \nl$

Na řešení se podívej až to doděláš sám. Zobrazit/skrýt!

PS: Nezapomeň u této rovnice provést zkoušku!

vonSternberk · 11. 05. 2009 12:10

díky...muzete jeste zkontrolovat někdo toto: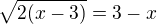
$\sqrt{2(x-3)}=3-x$
$2(x-3)=9-6x+x^2$
$2x-6=9-6x+x^2$
$-x^2+8x-15$
$-(x^2-8x+15)$
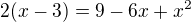
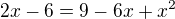
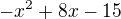
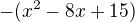
...diskriminant mi vyšel 4
...a kořeny 5,3
...tzn. řešením jsou čísla 5,3

gadgetka

$x^2-8x+15=0\nlx_{1,2}=\frac{8\pm \sqrt{64-60}}{2}=\frac{8\pm 2}{2}\nlx_1=5\nlx_2=3$

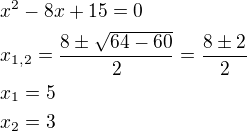
Řešení máš dobře, jen bych nevytýkala mínus, když mám na jedné straně rovnice záporný kvadratický člen, je jednodušší ho jen dát na stranu druhou :)) (a dodatečně koukám, že vlastně kvadratický člen vůbec záporný nebyl)

a dopiš si k rovnicím =0 tam, kde dáváš všechny členy na jednu stranu, na druhé straně zbyde nula (pokud bys členem z jedné strany rovnice dělil člen na straně druhé, na opačné straně zbyde jednička :) )

vonSternberk · 11. 05. 2009 12:31

to jsem rád, že ti to vyšlo stejně, ale vysledek má být POUZE x=3, jinak dík za připomínky

gadgetka · 11. 05. 2009 12:32

podmínky!

gadgetka

$2(x-3)\ge 0\nl x-3\ge 0\nl x\ge 3$

Podmínka pro umocnění:
$3-x\ge 0$
$x\le 3$

gadgetka · 11. 05. 2009 12:34

↑ vonSternberk:

3 nebo 5? :)

vonSternberk · 11. 05. 2009 12:54

právě, že kořen 3 je řešením rovnice, kdežto 5 není:(

marnes · 11. 05. 2009 14:01

↑ vonSternberk:

Matematické Fórum

#1 19. 04. 2009 12:01

Iracionální rovnice

#2 19. 04. 2009 12:03

Re: Iracionální rovnice

#3 19. 04. 2009 14:24 — Editoval matoxy (19. 04. 2009 14:33)

Re: Iracionální rovnice

#4 19. 04. 2009 14:36

Re: Iracionální rovnice

#5 19. 04. 2009 17:42 — Editoval joker (19. 04. 2009 19:46)

Re: Iracionální rovnice

#6 19. 04. 2009 18:18

Re: Iracionální rovnice

#7 19. 04. 2009 18:25

Re: Iracionální rovnice

#8 19. 04. 2009 19:09

Re: Iracionální rovnice

#9 19. 04. 2009 19:12

Re: Iracionální rovnice

#10 19. 04. 2009 19:14

Re: Iracionální rovnice

#11 19. 04. 2009 19:44

Re: Iracionální rovnice

#12 07. 05. 2009 10:21

Re: Iracionální rovnice

#13 07. 05. 2009 10:30

Re: Iracionální rovnice

#14 07. 05. 2009 10:32

Re: Iracionální rovnice

#15 10. 05. 2009 12:03

Re: Iracionální rovnice

#16 10. 05. 2009 12:12

Re: Iracionální rovnice

#17 11. 05. 2009 12:10

Re: Iracionální rovnice

#18 11. 05. 2009 12:18 — Editoval gadgetka (11. 05. 2009 12:20)

Re: Iracionální rovnice

#19 11. 05. 2009 12:31

Re: Iracionální rovnice

#20 11. 05. 2009 12:32

Re: Iracionální rovnice

#21 11. 05. 2009 12:33 — Editoval gadgetka (02. 07. 2016 22:51)

Re: Iracionální rovnice

#22 11. 05. 2009 12:34

Re: Iracionální rovnice

#23 11. 05. 2009 12:54

Re: Iracionální rovnice

#24 11. 05. 2009 13:32 Příspěvek uživatele gadgetka byl skryt uživatelem gadgetka. Důvod: již zbytečné

#25 11. 05. 2009 14:01

Re: Iracionální rovnice

Zápatí