Matematické Fórum

Crashatorr · 08. 12. 2014 18:29

Zdravím, poprosil bych někoho o pomoc s následujícím příkladem.

Vypočti obsah rovinné plochy vymezený křivkami zadanými parametricky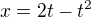

$x=2t-t^{2}$ , $y=2t^{2}-t^{3}$

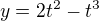
Znám vzorec, zintegrovat mi to taky nedělá problém, ale většinou nejsem schopen určit meze u křivek které jsou zadány parametricky. Je na to nějaký obecný postup? Nějak jsem to buď nepochytil nebo nám to nikdo ani neřekl, tak budu rád za každou radu

Jj · 09. 12. 2014 12:21

↑ Crashatorr:

Dobrý den.

Řekl bych, že jde o jednu křivku - tvar viz Odkaz, takže zřejmě obsah té "smyčky" (označím ji 'c').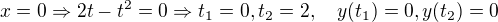

$x = 0 \Rightarrow 2t-t^2 = 0\Rightarrow t_1 = 0, t_2 = 2,\quad y(t_1) = 0, y(t_2)=0$

Roste-li parametr od 0 do 2, obíhá bod (x, y) křivku ve směru rostoucího parametru (tj. v kladném směru), oběhne ji právě jednou.

Pro tento případ je dobré znát a použít vzorec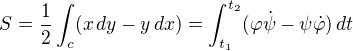

$S = \frac{1}{2}\int_c(x\,dy-y\,dx)=\int_{t_1}^{t_2}(\varphi\dot{\psi}-\psi\dot{\varphi})\,dt$

kde x = fí(t), y = psí(t) jsou parametrické rovnice křivky 'c'.

Poznámka: Vzorec se použije také pro obsah výseče mezi průvodiči krajních bodů části křivky 'c' (mezemi v integrálu budou hodnoty parametru v těchto bodech).

Matematické Fórum

#1 08. 12. 2014 18:29

Obsah plochy ohraničený křivkami

#2 09. 12. 2014 12:21

Re: Obsah plochy ohraničený křivkami

Zápatí