Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 12. 2014 17:39
Lagrangeovi multiplikátory
Hoj, věděl by někdo o programu podobně jako je MAW, mathway, wolframalpha. Který by dokázal spočítat lagrangeovi multiplikátory (s postupem nebo bez). Já je počítám, ale tím jak už nemám správné výsledky tak zrovna u tohohle nevím, jestli jsem to spočítal správně nebo špatně, když vyjdou des. čísla.
Offline
#2 21. 12. 2014 20:23 — Editoval jelena (20. 01. 2015 22:44)
Re: Lagrangeovi multiplikátory
Ještě to doplním o příklad, který mi vrtá hlavou a nedaří se spočítat.
vazba č1. 
vazba č.2 
Edit: podrobné řešení od kolegy Rumburaka Odkaz
provedl jsem derivace s úpravou lambd na:


Mě to stále vychází, že 
což je 
a pak mi z toho vyjde že 

a  dopočítám z vazby č.2 tj.
dopočítám z vazby č.2 tj. 
Problém je, že to takhle vyjít nemá, ale nevím, kde je chyba :(
Offline
#3 22. 12. 2014 10:40
#5 22. 12. 2014 12:46 — Editoval blak (22. 12. 2014 19:04)
Re: Lagrangeovi multiplikátory
↑ Eratosthenes:
No odmocnil jsem výraz vpravo, abych získal  samotnout. Což ale znamená, že jsem to odmocnil špatně. Jak by vypadalo správné odmocnění ?
samotnout. Což ale znamená, že jsem to odmocnil špatně. Jak by vypadalo správné odmocnění ?
↑ Jj:
Aha, já zkoušel WA, ale psal jsem tam "lambda" a to mi neschroustal. Je program co umí i postup ?
Popř. mohl by mi zde někdo uvést daný postup vyjádření  a
a  v zadaném příkladu, já se s tou odmocninou nedokážu hnout :(
v zadaném příkladu, já se s tou odmocninou nedokážu hnout :(
Offline
#7 23. 12. 2014 00:07 — Editoval jelena (20. 01. 2015 22:39)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lagrangeovi multiplikátory
Zdravím,
ohledně "programu s postupem" (předpokládám, že rovnou k použití, bez většího zásahu uživatele) přesunu do sekce CAS (řekla bych, že kontrola WA může být dostačující).
Ohledně odmocnění 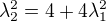 platí
platí  , ale nekontrolovala jsem, zda se k tomuto šlo dobře. Jelikož ohledně samotné úlohy bych 1. vazbu
, ale nekontrolovala jsem, zda se k tomuto šlo dobře. Jelikož ohledně samotné úlohy bych 1. vazbu  dosadila do předpisu funkce
dosadila do předpisu funkce  a do Lagrange bych použila jen druhou vazbu (edit: dosazovat se může, ale počet vazeb musí zůstat zachován Odkaz). Může být? Děkuji.
a do Lagrange bych použila jen druhou vazbu (edit: dosazovat se může, ale počet vazeb musí zůstat zachován Odkaz). Může být? Děkuji.
Offline
#9 26. 12. 2014 11:22
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lagrangeovi multiplikátory
blak napsal(a):
Tedy, já ani netušil,
"There are more things in heaven and earth, Horatio, ..." (c)
Zkus si uvědomit, co znamená vyšetření extrému funkce vice proměnných na zadané vazbě (i včetně geometrické interpretace) - bude jasné. Samozřejmě, pokud je úloha na procvičení metodiky LM na více vazeb a více lambd, tak dosazování spíš použiješ jako kontrolní metodu.
Je dořešeno? Děkuji.
Offline
#10 16. 01. 2015 23:22
Re: Lagrangeovi multiplikátory
Dořešeno není, musel jsem od toho na několik dní ustoupit, ale vypadá to, že LM je snad dělaný, aby se v něm člověk ztratil. Někde dělám chybu a proto mi to nevychází, zkusím to ještě párkrát spočítat a dám sem svůj postup, třeba zde tvé bystré oko hned uvidí v čem opakuji chybu. A začínám si i myslet, že jsou 3 -4 typy výpočtů, jedno, kdy si vyjádřím Lambdu u dvou ze tří rovnic a dosadím do zadání a tím získám jednu proměnou. Další, kde si vyjádřím x,y,z pomocí Lambd. Pak rovnice od sebe odečtu a pak je jedna, která mi stále uniká, protože koukám hodinu na zadání a nemyslím si, že se dá něčím vůbec něco vyjádřit. TO je následující zadání, kde nejde nic vyjádřit:
g1: 
g2: 
Jediné k čemu jsem se dostal bylo rozepsání rovnic:
x: 
y: 
z: 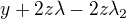
Offline
#11 16. 01. 2015 23:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lagrangeovi multiplikátory
↑ blak:
Také pozdrav,
Jediné k čemu jsem se dostal bylo rozepsání rovnic:
rovnice je od "rovná se", to chybí.
 odsud
odsud  (2)
(2) odsud
odsud  (3)
(3)
(2) s (3) můžeš podělit levé a pravé strany, nebo z (2) vyjádřit 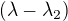 a dosadit do (3), dostaneš
a dosadit do (3), dostaneš 
K tomu  (4)
(4) (5)
(5)
To už by se mělo podařit, celá (5) jde dosadit do (4) (a to už se dalo i při převodu jen na jednu vazbu).
musel jsem od toho na několik dní ustoupit
tak do toho můžeš opět nastoupit :-)
Offline
#12 17. 01. 2015 14:54
Re: Lagrangeovi multiplikátory
Zdravím,
Tak s Vaší pomocí jsem dopočítal př. ze včera, jen nastíním postup, jestli byl správný, podle výsledký z WA, by měl sedět, ale zda jsem se k němu propracoval správně netuším :)
Ze vztahu 
Jsem následně odečetl jednu vazbu od druhé a vznikla mi kvadr. rovnice 
z vazby g2: jsem vyjádřil, že 
a dosadil jsem do ní  a vyšlo mi
a vyšlo mi 
následně jsem zadal  a
a  do vazby g1: abych získal
do vazby g1: abych získal 
A zde přikládám odkaz na max. a min. podle WA Odkaz
Byl můj postup správný, nebo jsem na výsledek přišel opět jen čirou náhodou ? :(
Offline
#14 17. 01. 2015 17:59 — Editoval blak (17. 01. 2015 21:28)
Re: Lagrangeovi multiplikátory
jelena napsal(a):
Zdravím,
ohledně "programu s postupem" (předpokládám, že rovnou k použití, bez většího zásahu uživatele) přesunu do sekce CAS (řekla bych, že kontrola WA může být dostačující).
Ohledně odmocněníplatí
, ale nekontrolovala jsem, zda se k tomuto šlo dobře. Jelikož ohledně samotné úlohy bych 1. vazbu
dosadila do předpisu funkce
a do Lagrange bych použila jen druhou vazbu. Může být? Děkuji.
Zkusil jsem znovu první příklad, "můj" postup mě stále dostává do smyčky. Zkusil jsem proto Váš s dosazením první vazby do zadání, nejspíš jsem to udělal špatně.
vzešlo mi zadání 
podle toho jsem udělal derivace:
x: 
y: 
z: 
vazba g2: 
Ale tam se nedá nic vyjádřit, krom  . A to pak už dál nevím co dělat :(
. A to pak už dál nevím co dělat :(
Ještě bych se rád zeptal, je nějaký způsob, jak si ověřit, že dané body jsou správné a jsou oním řešením ?
Následně se marně snažím nalézt odpověď na "Jak vytvořím vazbu pro Lagrange, pokud mám zadané jen body ![kopírovat do textarea $[1,5], [4,2]$](/mathtex/23/234e764cf0db911f647f80137bece271.gif) nebo nerovnosti typu :
nebo nerovnosti typu : 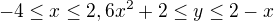 . Protože LM má být univerzální metodou, to je jen zajímavost pro mě, protože každý mi jen odepsal "nezkoumej to a dělej to dosazovací"
. Protože LM má být univerzální metodou, to je jen zajímavost pro mě, protože každý mi jen odepsal "nezkoumej to a dělej to dosazovací"
Počítal jsem další příklad
pomocí odečtení dvou vazeb jsem zíískal : 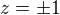
následně se vrátil k vyjádřenému  a zjistil, že
a zjistil, že 
Ale pak mi z vazby g1 vyšlo, že 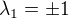
Ovšem pak mi nevychází správné  a
a 
Které má být dle řešení a
a 
Ale jak se tam dostala ta odmocnina nechápu, protože v mém postupu jsem dostal to samé, ale bez ní.
Offline
#15 17. 01. 2015 23:24 — Editoval jelena (18. 01. 2015 00:16)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lagrangeovi multiplikátory
↑ blak:
1) nevzešlo
vynecháváš v zápisu f(x, y, z)=... Máme:
funkce  , vazba
, vazba  a vazba
a vazba  .
.
Po dosazení vychází funkce  a druhá vazba
a druhá vazba  ,
,  ,
,  . Potom máme soustavu
. Potom máme soustavu 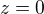


-------------------
2) body ![kopírovat do textarea $[1,5], [4,2]$](/mathtex/23/234e764cf0db911f647f80137bece271.gif) - také bych je dosazovala, ale pokud trváš na Lagrange, tak snad vytvořit předpis vazbových funkcí tak, aby jejich průsečíkem byly pravě takové body? Např. 2 kružnice.
- také bych je dosazovala, ale pokud trváš na Lagrange, tak snad vytvořit předpis vazbových funkcí tak, aby jejich průsečíkem byly pravě takové body? Např. 2 kružnice.
nebo nerovnosti 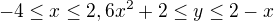 . Zde zadáváš oblast, tedy Lagrange vyřešit hranici oblasti a ještě jinou metodou vyšetřit vnitřek oblasti.
. Zde zadáváš oblast, tedy Lagrange vyřešit hranici oblasti a ještě jinou metodou vyšetřit vnitřek oblasti.
K té otázce 2) si založ, prosím, samostatné téma, bude lepší, když na takové dotazy bude odpovídat odborně zdatný kolega, než já.
---------------------------------------------
3)  tak se to nepíše. Má být
tak se to nepíše. Má být 
mně to vyšlo dle výsledku (pokud jsem neudělala nějakou chybu),  mám také,
mám také,
potom jsem měla rovnice s vazbou (výsledek po derivování):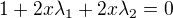

zde jsem dosadila  a použila stejnou techniku jako ↑ příspěvek 11:, tedy jsem
a použila stejnou techniku jako ↑ příspěvek 11:, tedy jsem  nepotřebovala. Dokončila jsem použitím
nepotřebovala. Dokončila jsem použitím  .
.
Offline
#16 18. 01. 2015 10:51 — Editoval blak (18. 01. 2015 13:20)
Re: Lagrangeovi multiplikátory
jelena napsal(a):
↑ blak:
1) nevzešlo
vynecháváš v zápisu f(x, y, z)=... Máme:
funkce, vazba
a vazba
.
Po dosazení vychází funkcea druhá vazba
,
,
. Potom máme soustavu
-------------------
Takže i když ze dvou vazeb použiju jednu do zadání, abych měl jen jednu lambdu, tak stále pak v rozvětvení rovnic počítám se dvěma ? Nepočítám pak jen s tou jednou, kterou jsem nepoužil do zadání ?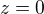
 s touhle jsem pak už v dalším počítání nepočítal, protože jsem si myslel že použitím, se vyřazuje z výběru.
s touhle jsem pak už v dalším počítání nepočítal, protože jsem si myslel že použitím, se vyřazuje z výběru.
Když jsem počítal s oběmi vazbami, tak mi vyšlo glob. min. ![kopírovat do textarea $[3,-1,0]$](/mathtex/0a/0a99d1c728d13f4647bf596c5cb75d37.gif) a
a ![kopírovat do textarea $[-3,1,0]$](/mathtex/50/503f9a7674db287dc828bcd13e9d9980.gif)
Ale jak mám následně přijít na glob. max. které je dle řešení ![kopírovat do textarea $[-1,-3,2]$](/mathtex/e3/e39d8d1d903ea3e623b1d8b3559b49e5.gif) ?
?
zde jsem dosadila
a použila stejnou techniku jako ↑ příspěvek 11:, tedy jsem
nepotřebovala. Dokončila jsem použitím
.
Můžu se zeptat jak jste se mohla obejít bez vyjádření  , když právě zadáním do rovnice
, když právě zadáním do rovnice 
 Z toho jde vyjádřit přeci pouze ona
Z toho jde vyjádřit přeci pouze ona 
Offline
#17 18. 01. 2015 13:26 — Editoval jelena (20. 01. 2015 22:41)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lagrangeovi multiplikátory
↑ blak:
pořád zůstává vztah mezi x, y,  , který se použije pro další výpočty.
, který se použije pro další výpočty.
Bohužel ale máš pravdu - tou moji metodou se část bodů ztrácí. Ale nevím, v kterém místě úvah by mohla být chyba (edit: odůvodněno zde - dosazovat se může, ale počet vazeb musí zůstat zachován Odkaz). Vazba  a
a  zadávají elipsu, která vznikne řezem nekonečného válce rovinou. Na této elipse hledáme extrémy
zadávají elipsu, která vznikne řezem nekonečného válce rovinou. Na této elipse hledáme extrémy  .
.
Při užití jedné vazby  k dosazování do
k dosazování do  (což je množina sfér se středem 0,0,0) bych měla dostat opět nekonečný válec a ten vyšetřuji na extrém na rovině, která ho přetne v elipse. A tak nevím, jak bych zdůvodnila ztrátu bodů. měla jsem za to, že mohu dosazovat vazbu do zadání, nebo vazbu do vazby.
(což je množina sfér se středem 0,0,0) bych měla dostat opět nekonečný válec a ten vyšetřuji na extrém na rovině, která ho přetne v elipse. A tak nevím, jak bych zdůvodnila ztrátu bodů. měla jsem za to, že mohu dosazovat vazbu do zadání, nebo vazbu do vazby.
Tak tuto cestu raději zanech a pokračuj vyšetřování před 2 lambdy (tam všechno vychází). Počkám, zda někdo z kolegů nevnese jasno, kde jsem měla chybu v úvaze o dosazování, kolegům děkuji.
Offline
#18 18. 01. 2015 15:29
Re: Lagrangeovi multiplikátory
No, stále lepší mít polovinu bodů za příklad v testu než žádné body, protože s těma dvěma lambdama nedostanu ani jednu část příkladu. Celkově si stejně nědělám naděje, že bych test dal, takže bude opáčko za rok. Vyjde mi tak 1 příklad z 15. A to jsem ani nezačal počítat ty o základu  nebo
nebo  ,
, 
Offline
#19 18. 01. 2015 18:33
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lagrangeovi multiplikátory
↑ blak:
to ne, můj návrh musí být chybný - tedy i polovina bodů získaných nesprávnou metodou nebude správné řešení. Sice pořád si myslím, že bych mohla alespoň spojovat vazby, ale neber na to ohled.
Funkci sestavit umíš, zderivovat také, problém je v samotném řešení soustavy rovnic - to se bohužel vleče odněkud ze SŠ a zde se jen používá. Zkus se možná podívat na přehled metodik - zda např. Jakobiánem bys to neviděl přehlednější (ale je to opět o rovnici - věděl bys však, že potřebuješ rozložit na součin).
Offline
#20 19. 01. 2015 12:28
Re: Lagrangeovi multiplikátory
To pdf jsem si prošel, ale bohužel pro mě, tam není ukázka LM při dvou vazbách, takže když se pak v příkladu jako je ten první, který je naprosto nesmyslný a dohání mě k šílenství, tak se obdobně vyskytují snad ob příklad. Př. 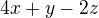
g1:
g2:
tedy vznikne:


zadal jsem to do g2 a z toho vzešlo:  , což je mi k ničemu, protože se s tím dál počítat opět nedá a takhle je to u 98% příkladů co se snažím spočítat. Vždy to vyústí ve slepou cestu. Jen se divím, jak někdo dokáže vystudovat obory, které se na tomhle zakládají a nezcvoknout se.
, což je mi k ničemu, protože se s tím dál počítat opět nedá a takhle je to u 98% příkladů co se snažím spočítat. Vždy to vyústí ve slepou cestu. Jen se divím, jak někdo dokáže vystudovat obory, které se na tomhle zakládají a nezcvoknout se.
Offline
#21 19. 01. 2015 13:06 — Editoval jelena (20. 01. 2015 22:43)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lagrangeovi multiplikátory
↑ blak:
Zdravím, můžeš dosadit do třech posledních rovnic (kde je vyjádření x, y, z), potom x, y, z jsou závislé jen na
můžeš dosadit do třech posledních rovnic (kde je vyjádření x, y, z), potom x, y, z jsou závislé jen na  a to půjde dosadit do
a to půjde dosadit do  (při trošce úprav vznikne kvadratická rovnice, najdeš
(při trošce úprav vznikne kvadratická rovnice, najdeš  ).
).
Nebo dosadit  do rovnic:
do rovnic: (3)
(3) (4)
(4) (5)
(5)
Potom po vyjádření  půjde opět použit poměry, jak jsme dělali v předchozích soustavách.
půjde opět použit poměry, jak jsme dělali v předchozích soustavách.
-----------------
Možna bych zkusila i tak: celá soustava je:  (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5)
-----------------------
zkontroluji počty neznámých (mám 5 rovnic, 5 neznámých), vidím, že 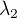 je osamostatněna v (3), (4), (5), tedy sečtením (3) a (4), (4)a(5), (3)a(5) (případně s vhodným vynásobením) "vyruším"
je osamostatněna v (3), (4), (5), tedy sečtením (3) a (4), (4)a(5), (3)a(5) (případně s vhodným vynásobením) "vyruším" 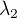 , zkus se podívat, zda to není pohodlnější. Ale Tvé rozpracování je také použitelné.
, zkus se podívat, zda to není pohodlnější. Ale Tvé rozpracování je také použitelné.
Na samotnou soustavu se ještě později podívat, také doufám, že se mi dostane kritiky v metodě dosazování vazby od odborně zdatného kolegy, již teď děkuji. (edit: kritiky se dostalo + podrobné řešení Odkaz)
Offline
#22 19. 01. 2015 13:38 — Editoval blak (19. 01. 2015 13:46)
Re: Lagrangeovi multiplikátory
Dobře i přez počáteční rozpaky, že by mi nemělo vyjít  a s ním dál počítat, jsem to tedy udělal a vyšlo mi
a s ním dál počítat, jsem to tedy udělal a vyšlo mi 
z toho následně 


To bylo při dosazení do vazby g2. Při dosazení do g1 mi vyjde pod odmocninou záporné číslo 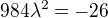
Což jsou krásná celá čísla, problém je, že to nejsou ty, která mají vyjí správně tedy :  a
a 
Offline

 ?
? .
.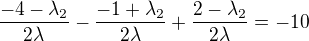 , a tak
, a tak  . Jak to vypadá? Děkuji.
. Jak to vypadá? Děkuji.
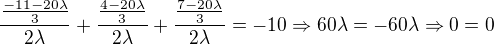



 , doporucuji substituci
, doporucuji substituci  .
.