Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 29. 12. 2014 11:06
Re: integrál
↑ Booback:
Ahoj.
Na to se dá nejsnáze přijít z definice primitivní funkce. Stačí si říct, co musíme zderivovat, abychom dostali  .
.
Offline
#3 29. 12. 2014 11:12 — Editoval Booback (29. 12. 2014 12:03)
Re: integrál
↑ Bati:
no, asi takhle.. kdybych to věděla, tak se tu neptám..jako je mi jasné, že ten výsledek co tam je, ale nemůžu a nemůžu na to přijít..uplně duto v té hlavě dneska mám :D a je mi jasné, že cos=sin, ale spíš mi vrtá hlavou ta 1/4 ? no nic, vyřešila jsem to substitucí a bylo..
Offline
#4 29. 12. 2014 12:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integrál
Zdravím,
je možná substituce asi
pokud máš na mysli "drobnou substituci" 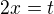 , tak určitě by se to pro Tebe zprůhlednilo. Z náhledu vidím, že jsi tak i vyřešila.
, tak určitě by se to pro Tebe zprůhlednilo. Z náhledu vidím, že jsi tak i vyřešila.
jestli není i nějaký vzorec pro toto?
V bílé knize v černých polích :-)
a je mi jasné, že cos=sin,
jen občas.
Offline


