Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 01. 2015 19:38
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Limita funkce
Dobrý den, pomůžete mi prosím s touto limitou funkce?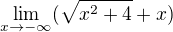 .
.
Nejprve jsem vše vynásobila stejným výrazem akorát s  . Vyšlo mi:
. Vyšlo mi:  . Poté jsem vytkla
. Poté jsem vytkla  pod odmocninou a částečně odmocnila. Vyšlo mi
pod odmocninou a částečně odmocnila. Vyšlo mi  . Pokud nyní ale dosadím
. Pokud nyní ale dosadím  vyjde mi ve jmenovateli neurčitý výraz
vyjde mi ve jmenovateli neurčitý výraz  Poradíte mi prosím, co s tím nebo kde mám chybu? Moc děkuji.
Poradíte mi prosím, co s tím nebo kde mám chybu? Moc děkuji.
Offline
- (téma jako vyřešené označil(a) terezkaaaaa5)
#2 06. 01. 2015 19:49 — Editoval Pavel (06. 01. 2015 19:49)
Re: Limita funkce
↑ terezkaaaaa5:
Problém je v tom, že v záporných číslech  se částečně odmocňuje jinak, a to
se částečně odmocňuje jinak, a to  . Důvod je ten, že
. Důvod je ten, že 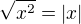 a absolutní hodnota se v záporných
a absolutní hodnota se v záporných  "odstraňuje" znaménkém
"odstraňuje" znaménkém  .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 06. 01. 2015 19:54
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Limita funkce
↑ Pavel:
Takže mi tedy ve jmenovateli vznikne  , tím pádem
, tím pádem 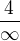 = 0?
= 0?
Offline
#4 06. 01. 2015 21:11
Re: Limita funkce
↑ terezkaaaaa5:
Ano.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
