Matematické Fórum

terezkaaaaa5 · 07. 01. 2015 16:23

Dobrý den pomůžete mi prosím s těmito příklady?

1) $\lim_{x\to2}\frac{x^{3}-8}{x^{4}-16}$

2) $\lim_{x\to0}\frac{\sqrt{x^{2}+x+1}}{x}$

U obou příkladů nevím jak začít a potřebovala bych poradit již s prvním krokem. Děkuji.

Argcotgh x · 07. 01. 2015 16:50

U té první bych začal rozkladem čitatele

$x^3-8=(x-2).(x^2+2x+4)$

a jmenovatele

$x^{4}-16=(x^2-4)(x^2+4)=(x-2)(x+2)(x+2)$

(x-2) v čitateli a jmenovateli se požere a pak už se snadno dopočítá.

terezkaaaaa5 · 07. 01. 2015 16:59

↑ Argcotgh x:

Moc děkuji. Nakonec to vyjde 3/4, že? Jen se chci zeptat (i když vím, že je to učivo střední. možná základní školy), jak vím, že ten čitatel rozložím přesně takto?

Argcotgh x · 07. 01. 2015 17:09

Většinou se zkouší co nejmenší celá čísla (přesně vzato, "kandidáti na kořeny" jsou všichni dělitelé absoulutního členu), tady je hned vidět, že je to 2 (2^3 - 8 = 0). Pak vydělím původní dvojčlen 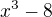$x^3-8$ "kořenovým činitelem" $x-2$ pomocí algoritmu dělení mnohočlenu mnohočlenem a získám tak $x^2+2x+4$ , celý rozklad je tedy $(x-2).(x^2+2x+4)$ .

terezkaaaaa5 · 07. 01. 2015 17:16

↑ Argcotgh x:

Skvěle vysvětleno, moc děkuji.

A víte i jak na tu druhou limitu prosím? :)

vlado_bb · 07. 01. 2015 17:24

↑ terezkaaaaa5:vo vyraze pod odmocninou vyber $x^2$ .

Argcotgh x · 07. 01. 2015 17:29

Napadá mě ne zrovna košer způsob, l'Hospitalovo pravidlo - zvlášť zderivuju čitatele i jmenovatele.

$\lim_{x\to0}\frac{\sqrt{x^2+x+1}}{x}=\lim_{x\to0}\frac{\frac{2x+1}{2\sqrt{x^2+x+1}}}{1}=\lim_{x\to0}\frac{2x+1}{2\sqrt{x^2+x+1}}$

$\lim_{x\to0}\frac{2x+1}{2\sqrt{x^2+x+1}}=\frac{2.0+1}{2\sqrt{0^{2}+0+1}}=\frac{1}{2\sqrt{1}}=\frac{1}{2}$

Určitě to jde jinak a lépe (možná i jednodušeji), ale zrovna mě nenapadá.

terezkaaaaa5 · 07. 01. 2015 17:29

↑ vlado_bb:

Zbude mi $\sqrt{1+\frac{1}{x}+\frac{1}{x^{2}}}$ Jenže dosadit nulu za x stále nemůžu

terezkaaaaa5 · 07. 01. 2015 17:30

↑ Argcotgh x:

Díky, ale zapomněla jsem dodat, že mám řešit bez použití l'Hospitalova pravidla

Argcotgh x · 07. 01. 2015 17:34

↑ terezkaaaaa5:

Jasně, chápu, jen mě teď nic lepšího nenapadlo. S těmi x = 0 ve jmenovateli si nedokážu poradit :-(

jarrro · 07. 01. 2015 17:37 — Editoval jarrro (07. 01. 2015 17:38)

veď čitateľ ide k 1 menovateľ k 0 a čitateľ je v okolí nuly stále kladný a menovateĺ mení znamienko teda limita neexistuje
Lhospitalovu vetu nemôžeš používať, lebo nie sú splnené jej predpoklady

vlado_bb · 07. 01. 2015 17:38

↑ terezkaaaaa5:Aha, to je limita v nule. Si si ista, ze to nema byt v nekonecne? Ak naozaj v nule, tak je to lahke, vyjde to z definicie limity. A mimochodom, to, co pisal ↑ Argcotgh x: je cele zle.

terezkaaaaa5 · 07. 01. 2015 17:40

↑ vlado_bb:

Dobře děkuji.

Argcotgh x · 07. 01. 2015 17:41

Už vidím svou blbost - na l'Hospitala je třeba, aby byla limita "0/0", což není. Moc se omlouvám.

terezkaaaaa5 · 07. 01. 2015 19:46

$\lim_{x\to3}\frac{\sqrt{x+13}-2\sqrt{x+1}}{x^{2}-9}=\lim_{x\to3}\frac{\sqrt{x+13}-2\sqrt{x+1}}{x^{2}-9}\cdot \frac{\sqrt{x+13}+2\sqrt{x+1}}{\sqrt{x+13}+2\sqrt{x+1}}= \lim_{x\to3}\frac{x+13-4(x+1)}{(x-3)(x+3)(\sqrt{x+13}+2\sqrt{x+1})}=\lim_{x\to3}\frac{-3x+9}{jmenovatel}=\lim_{x\to3}\frac{-3(x-3)(\sqrt{x+13}+2\sqrt{x+1})}{jmenovatel}=\lim_{x\to3}\frac{-3}{(x+3)\cdot (\sqrt{x+13}+2\sqrt{x+1})}= \lim_{x\to3}\frac{-3}{6(4+2.2)}=-\frac{3}{48}=-\frac{1}{16}$

jelinekgreen · 07. 01. 2015 21:50

↑ terezkaaaaa5:
Ta první vychází 3/8...

Matematické Fórum

#1 07. 01. 2015 16:23

Limita funkce

#2 07. 01. 2015 16:50

Re: Limita funkce

#3 07. 01. 2015 16:59

Re: Limita funkce

#4 07. 01. 2015 17:09

Re: Limita funkce

#5 07. 01. 2015 17:16

Re: Limita funkce

#6 07. 01. 2015 17:24

Re: Limita funkce

#7 07. 01. 2015 17:29

Re: Limita funkce

#8 07. 01. 2015 17:29

Re: Limita funkce

#9 07. 01. 2015 17:30

Re: Limita funkce

#10 07. 01. 2015 17:34

Re: Limita funkce

#11 07. 01. 2015 17:37 — Editoval jarrro (07. 01. 2015 17:38)

Re: Limita funkce

#12 07. 01. 2015 17:38

Re: Limita funkce

#13 07. 01. 2015 17:40

Re: Limita funkce

#14 07. 01. 2015 17:41

Re: Limita funkce

#15 07. 01. 2015 19:46

Re: Limita funkce

#16 07. 01. 2015 21:50

Re: Limita funkce

Zápatí