Matematické Fórum

terezkaaaaa5 · 07. 01. 2015 17:46

Dobrý den, mám funkci f(x) = 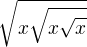$\sqrt{x\sqrt{x\sqrt{x}}}$ a mám ji zderivovat. Funkci jsem si upravila na: $x^{\frac{1}{2}}\cdot x^{\frac{1}{4}}\cdot x^{\frac{1}{8}}$ Je to prosím správně?

Jj · 07. 01. 2015 18:32

↑ terezkaaaaa5:

Zdravím.

Ano - výsledek $x^{7/8}$ je správný.

terezkaaaaa5 · 07. 01. 2015 18:37

↑ Jj:

a derivace tedy bude: $7/8\cdot x^{-\frac{1}{8}}$ ? :)

Argcotgh x · 07. 01. 2015 18:38

Podle mě je to správně,

zcela určitě platí např.

$\sqrt[m]{\sqrt[n]{\sqrt[p]{x}}}=\sqrt[m.n.p]{x}$

nebo pro tento případ

$\sqrt[m]{x\sqrt[n]{x\sqrt[p]{x}}}=\sqrt[m]{x}.\sqrt[m.n]{x}.\sqrt[m.n.p]{x}$

Argcotgh x · 07. 01. 2015 18:44

Aha, kolegové mě předběhli.

Derivace platí,

$(x^{\frac{7}{8}})' =\frac{7}{8}x^{\frac{7}{8}-\frac{8}{8}}=\frac{7}{8}x^{-\frac{1}{8}}$

Matematické Fórum

#1 07. 01. 2015 17:46

Derivace

#2 07. 01. 2015 18:32

Re: Derivace

#3 07. 01. 2015 18:37

Re: Derivace

#4 07. 01. 2015 18:38

Re: Derivace

#5 07. 01. 2015 18:44

Re: Derivace

Zápatí