Matematické Fórum

Crashatorr · 12. 01. 2015 14:11

Zdravím, chtěl bych se zeptat na jednu drobnost u Dedekindových řezů.
Máme Dedekindův řez, který má představovat číslo 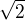$\sqrt{2}$
Zapíšeme ho tedy takto, označme ho třeba A $A=\{x\in\mathbb{Q}, x\cdot x<2\}$ .
Chtěl bych se zeptat na tuto věc, na jedné z přednášek jsme si to zapsali takhle, ale hned na následující přednášce náš přednášející doplnil ještě x<0 takže $A=\{x\in\mathbb{Q}, x\cdot x<2,x<0\}$ , nějak jsem to nepochytil a teď nemůžu přijít na to proč je třeba tam doplnit tu podmínku.

Rumburak · 12. 01. 2015 15:25

↑ Crashatorr:

Ahoj.

Má-li množina $A$ představovat dolní množinu řezu, pak mj. žádné rac. číslo nesmí být její dolní závorou.
Popsat ji pouze nerovností $x^2 < 2$ nestačí, protože taková množina rac. čísel má za dolní závoru např. $z = -10$ .
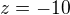Tyto nežáducí dolní závory vylouříme ze hry tím, že je přidáme do množiny $A$ . Její vyjádření pak bude jednoduše

$A=\{x\in\mathbb{Q}, x^2<2 \vee x < 0\}$ ,

Pro záporná čísla vyhovující nerovnici $x^2 < 0$ je sice podmínka $x < 0$ zbytečná a mohli bychom ji oslabit
třeba podmínkou $x < -1,4$ , anž by to na množinu $A$ mělo vliv, ale ani to není z uvedeného hlediska dokonalé.
Dokonalá by byla nerovnost 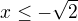$x \le -\sqrt{2}$ , ale tu zatím napsat nemůžeme, protože její pravá strana není
racionální číslo (a jiná čísla na tomto stupni Dedekindovy teorie nemáme).

Crashatorr · 12. 01. 2015 15:59

↑ Rumburak:
Děkuju za vysvětlení :)

Matematické Fórum

#1 12. 01. 2015 14:11

Dedekindovy řezy

#2 12. 01. 2015 15:25

Re: Dedekindovy řezy

#3 12. 01. 2015 15:59

Re: Dedekindovy řezy

Zápatí