Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 01. 2015 16:22 — Editoval frank_horrigan (18. 01. 2015 16:23)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Výpočet EV
Zdravím komunitu po delší době, co jsem se neukázal.
Měl bych tu relativně jednoduchou parametrickou rovnici, znám její kořeny, ale někde mi uteklo, jak se to upravilo tak, aby ten výsledný vzorec fungoval:
Je to výpočet očekávané hodnoty nějaké akce definované obecně takto:
Pro dvoustavový jev tedy platí rozklad ![kopírovat do textarea $EV = X * P(x) + Y * [1 - P(x)]$](/mathtex/d5/d55ef6ae3f9480f4373ec681df72df85.gif)
Nyní potřebuju vyšetřit, kdy se vyplatí provést akci, nazvěme jí call, tak, aby měla alespoň EV = 0. Je úloha z pokeru, snažím se nějak uchopit koncept impled odds (kdo hrají poker jistě ví co to je, ostatním zájemcům vysvětlím), a v tomto příkladu se řeší "čisté" pot odds.
Obecně platí, že pokud call udělám, tak buď vyhraju celý pot (parametr P), nebo prohraju svůj call, o kterém se rozhoduje (parametr C), funkce p je pravděpodobnost
Máme tedy výše uvedenou rovnici s našima parametrama: 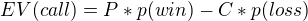
Potřeba vyšetřit, kdy se EV rovná nule: ![kopírovat do textarea $0 = P * p(win) - C * [1 - p(win)]$](/mathtex/7d/7d92089c54a737ed5fab867d265a8bd0.gif)
Doteraz chápenzí, ale následující dvě úpravy jsem nepochopil jak vznikly:¨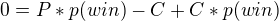
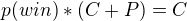
Z toho vypadne konečný vzorec: 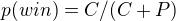 (a nepamatuju si jak se v texu dělají zlomky :D
(a nepamatuju si jak se v texu dělají zlomky :D
Může mi prosím někdo rozepsat, jak se ty dvě úpravy udělaly? Co s čím, co kam a proč?
Vím, že to je jednoduché, je to látka spíše základní školy, ale díky těm parametrům jsem se rozhodl to hodit spíše sem :)
Díky
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
- (téma jako vyřešené označil(a) frank_horrigan)
#2 18. 01. 2015 16:34 — Editoval vulkan66 (18. 01. 2015 16:36)
- vulkan66


- Místo: Praha
- Příspěvky: 416
- Škola: ČVUT FJFI - Částicová fyzika
- Pozice: student
- Reputace: 20
Re: Výpočet EV
↑ frank_horrigan:
Ahoj, moc nechápu co potřebuješ. Je to jenom jednoduchá úprava rovnic ne?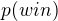 je
je 
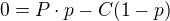


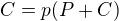
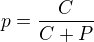
Vím, jak ovládat vesmír. Tak mi řekněte, proč bych se měl hnát za milionem? -Grigorij Perelman
Offline
#3 18. 01. 2015 16:48
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Výpočet EV
Jo, díky moc :)
Vím, že je to jednoduché, jen jsem to tam nějak nemohl najít, nedocvakávalo mi to :)
Díky, v této formě už to chápu.
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#4 18. 01. 2015 16:54
- vulkan66


- Místo: Praha
- Příspěvky: 416
- Škola: ČVUT FJFI - Částicová fyzika
- Pozice: student
- Reputace: 20
Re: Výpočet EV
↑ frank_horrigan:
Ok, není zač :)
Vím, jak ovládat vesmír. Tak mi řekněte, proč bych se měl hnát za milionem? -Grigorij Perelman
Offline