Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 01. 2015 00:36
Konvexní množina
Zdravím všechny, potřebovala bych poradit s následujícím příkladem.
Mám z definice konvexní množiny dokázat, že tato množina je konvexní: , kde A je pozitivně semidefinitní.
, kde A je pozitivně semidefinitní.
V předchozích příkladech jsme si vždycky zvolili dva vektory patřící do této množiny a a dokázali jsme, že tam patří i jejich konvexní kombinace. V tomhle případu si ale nejsem ale úplně jistá, jak to provést. Pokud si vezmu například nějaké vektory x a y a budu předpokládat, že: 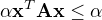
a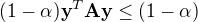
a to sečtu dostanu: 
tak mi není jasné, jak z tohoto dostanu požadovaný (nebo alespoň podle mě požadovaný) tvar: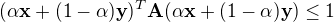
Jdu na to dobře? Špatně? Mám správné předpoklady?
Předem moc děkuju za odpověď.
Offline
#2 28. 01. 2015 10:36 — Editoval kafe_arabica (28. 01. 2015 10:36)
- kafe_arabica
- Příspěvky: 38
- Reputace: 3
Re: Konvexní množina
Ahoj.
Choď na to od konca. Roznásob si posledný riadok a odhaduj koeficienty a potom členy. Napr., vieš, že platí 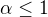 , rovnako
, rovnako 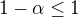 , a pre x,y platí
, a pre x,y platí 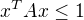 .
.
Offline
#4 28. 01. 2015 15:17
#6 09. 02. 2015 10:01
Re: Konvexní množina
↑ Neth:
A jak Ti vyšlo roznásobení výrazu  ? (Viz rada od ↑ kafe_arabica:)
? (Viz rada od ↑ kafe_arabica:)
Offline
#13 10. 02. 2015 11:29
Re: Konvexní množina
↑ Rumburak:
To naprosto chápu.
↑ jarrro:
Mohla bych se, prosím, zeptat, jak jsi k tomu došel?
Offline
#14 10. 02. 2015 11:52
Re: Konvexní množina
↑ Neth:
Jestliže z původních předpokladů 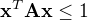 ,
, 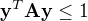 plyne i
plyne i 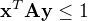
(viz můj dotaz ↑ Rumburak: na kolegu ↑ jarrro:), potom  .
.
O nezáporných číslech 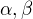 jsme přadpokládali, že jejich součet je 1.
jsme přadpokládali, že jejich součet je 1.
Offline
#15 10. 02. 2015 12:02
Re: Konvexní množina
↑ Rumburak:
Děkuju mnohokrát, už to tam vidím! Jen mám neblahý pocit, že 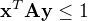 z toho automaticky neplyne.
z toho automaticky neplyne.
Offline
#18 11. 02. 2015 17:11
Re: Konvexní množina
Matica 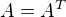 určuje na
určuje na  skalárny súčin
skalárny súčin 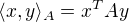 pre
pre 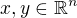 v prípade, že je pozitívne definitná. Pretože v našom uvažovanom prípade je
v prípade, že je pozitívne definitná. Pretože v našom uvažovanom prípade je  pozitívne semidefinitná neplatí
pozitívne semidefinitná neplatí  , avšak pri dôkaze Cauchy-Schwarzovej nerovnosti [1] sa tento fakt používa až pri určovaní podmienok pre rovnosť, preto ihneď máme
, avšak pri dôkaze Cauchy-Schwarzovej nerovnosti [1] sa tento fakt používa až pri určovaní podmienok pre rovnosť, preto ihneď máme
[1] napr. http://www.artofproblemsolving.com/Wiki … Inequality Proof1
Offline

 , kde matice
, kde matice 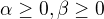 splňující
splňující  je
je  .
.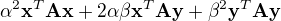
 .
.

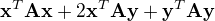 je vždy kladný nebo rovno nula (kvůli matici pozitivně semidefinitní)?
je vždy kladný nebo rovno nula (kvůli matici pozitivně semidefinitní)?