Matematické Fórum

terezkaaaaa5 · 29. 01. 2015 09:39

Dobrý den, pomůžete mi prosím s tímto příkladem? Moc děkuji předem.

$\lim_{x\to\infty } (\frac{x+a}{x})^{x}$

vlado_bb · 29. 01. 2015 09:51

↑ terezkaaaaa5:Pomohla by ti uprava $\lim_{x\to\infty } (1+\frac{a}{x})^{x}$ ? Pripomina ti to uz nieco?

terezkaaaaa5

vzorec $\lim_{x\to\infty } (1+\frac{1}{x})^{x}$ Ale jak s tím dál?

vlado_bb · 29. 01. 2015 09:57

↑ terezkaaaaa5:V LaTex-ovom pieskovisku si uvazovala spravnym smerom.

terezkaaaaa5 · 29. 01. 2015 09:58

↑ vlado_bb:

To mě napadlo, ale nevěděla jsem jestli to tak může být. A hlavně moc nevím, jak k tomu dojdu postupnými kroky? :)

vlado_bb · 29. 01. 2015 10:01

$\left (1+\frac{a}{x}\right )^{x}=\left (1 + \frac{1}{\frac xa}\right )^{\frac xa a}$ ... uz vidis?

terezkaaaaa5 · 29. 01. 2015 10:03

Jak jste došel k tomuto výrazu prosím? Moc jsem to bohužel nepochopila

vlado_bb

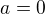↑ terezkaaaaa5:V zlomku vnutri zatvorky som citatela aj menovatela vydelil vyrazom $a$ . To sa moze, ak $a\ne 0$ . Lenze pre $a=0$ je dana limita problematikou materskej skoly, takze mozeme predpokladat ze $a \ne 0$ . No a v exponente som pouzil rovnost $x=\frac xa a$ . V dalsom kroku navrhujem pouzit rovnost $a^{bc}=(a^b)^c$ .

terezkaaaaa5 · 29. 01. 2015 10:15

↑ vlado_bb:

Dalším krokem už bude výsledek $\mathrm{e}^{a}$ , že? :)

vlado_bb

↑ terezkaaaaa5:Chybaju ti tam limity a aj ak ich tam doplnis, tak tretia rovnost nebude v poriadku, trochu to komplikujes :) (To este k tomu co si skryla - stihol som si pozriet ;) )

terezkaaaaa5 · 29. 01. 2015 10:22

↑ vlado_bb:

Do toho zápisu, který jsem skryla, se mi vmíchalo něco navíc. To, že mi tam chyběly limity vím :) Každopádně po zadání následuje 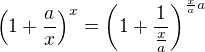$\left (1+\frac{a}{x}\right )^{x}=\left (1 + \frac{1}{\frac xa}\right )^{\frac xa a}$ a pak výsledek $\mathrm{e}^{a}$ , že? :)

vlado_bb · 29. 01. 2015 10:30

↑ terezkaaaaa5:Ano, mozno by som to este napisal ako $\left (1+\frac{a}{x}\right )^{x}=\left (1 + \frac{1}{\frac xa}\right )^{\frac xa a}=\left [ \left (1 + \frac{1}{\frac xa}\right )^{\frac xa}\right ]^a$ aby tomu rozumel skutocne kazdy.

Matematické Fórum

#1 29. 01. 2015 09:39

Limity funkce

#2 29. 01. 2015 09:51

Re: Limity funkce

#3 29. 01. 2015 09:55 — Editoval terezkaaaaa5 (29. 01. 2015 09:56)

Re: Limity funkce

#4 29. 01. 2015 09:57

Re: Limity funkce

#5 29. 01. 2015 09:58

Re: Limity funkce

#6 29. 01. 2015 10:01

Re: Limity funkce

#7 29. 01. 2015 10:03

Re: Limity funkce

#8 29. 01. 2015 10:06 — Editoval vlado_bb (29. 01. 2015 10:07)

Re: Limity funkce

#9 29. 01. 2015 10:11 Příspěvek uživatele terezkaaaaa5 byl skryt uživatelem terezkaaaaa5.

#10 29. 01. 2015 10:15

Re: Limity funkce

#11 29. 01. 2015 10:15 — Editoval vlado_bb (29. 01. 2015 10:16)

Re: Limity funkce

#12 29. 01. 2015 10:22

Re: Limity funkce

#13 29. 01. 2015 10:30

Re: Limity funkce

Zápatí