Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 01. 2015 20:20
Slovní úlohy o pohybu - interpretace
Zdravím,
holka chodí na gympl a přinesla trojku z matematiky. Problém je prý ve slovních úlohách o pohybu, směsích, společné práci apod. a jejich správné interpretaci. Přiznám se, že nejsem na matematiku nijak zvlášť zaměřený, takže nejsem schopen jí s tím poradit. Dám sem dvě typické úlohy a potřeboval bych nějak nasměrovat či poradit, jak takové věci řešit.
1. Ivan urazil na kole trať dlouhou 96 km v čase o 2 hodiny kratším, než původně předpokládal. Přitom za každou hodinu ujel o 1 km více, než měl původně urazit za 1 h 15 min. Jakou rychlostí Ivan skutečně jel?
2. Dva kopáči mají vykopat příkop. Kdyby každý z nich pracoval právě třetinu té doby, kterou by k výkopu potřeboval druhý kopáč, vykopali by dohromady 13/18 příkopu. Určete, v jakém poměru jsou výkonnosti obou kopáčů.
Prosím vás, tohle jsou ukázkové úlohy, zkuste mi to vysvětlit nějak laicky, popř. mě nasměrovat na nějaké podrobnější vysvětlení. Kdybyste přidali postup řešení u těchto dvou ukázkových úloh, byl bych velmi vděčný.
Díky, Jirka
Offline
#2 29. 01. 2015 21:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úlohy o pohybu - interpretace
Zdravím,
hodně podrobně rozebírá typy úloh pan Krynický (v kapitolách Lineární rovnice a Kvadratické rovnice). Zkuste projít, zda pomůže a zda se podařilo některou z uvedených poskládat a interpretovat (u pohybu je dobré kreslit obrázek). Některý ochotný spolužák na doučování by se nenašel? Děkuji.
Offline
#3 30. 01. 2015 11:06
Re: Slovní úlohy o pohybu - interpretace
↑ Lokutus:
Dobrý den.
První příklad je rozveden tady: Příklad 7
Pokud se tedy nemýlím.
Offline
#4 30. 01. 2015 12:50
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úlohy o pohybu - interpretace
↑ Jj:
Zdravím Vás a děkuji, to je ze stejného zdroje, co kolegovi nabízím studovat podrobně. S autorem odkazované elektronické učebnice panem Krynickým jsme rozsáhlejší spolupráci nenavázali, ale je zde (v sekci Didaktiky) téma k účebnici, kde také odpovídá a vyzývá i k reakcím na učebnici.
Offline
#5 12. 10. 2018 12:23
- petrik_ch

- Místo: Topoľčany
- Příspěvky: 241
- Škola: ZS Tribecska Topolcany
- Pozice: priatel skoly, absolvent, rodic
- Reputace: 2
- Web
Re: Slovní úlohy o pohybu - interpretace
Priklad c.2. je i s postupem vyresen:
https://www.hackmath.net/cz/priklad/7015
Offline
#6 12. 10. 2018 19:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úlohy o pohybu - interpretace
↑ petrik_ch:
Zdravím,
nejde v zápisu řešení nějak ošetřit, aby racionální číslo zůstávalo v původním tvaru po celou dobu úprav, včetně všech odvození - matematických operací prováděných s použitím tohoto čísla? Pokud si vzpomínám, tak číselné výpočty pro "vzorové úlohy" byly prováděny přes WA, tedy by šlo určit tvar čísla. Nebo to ošetřit ručně.
Není možné prezentovat vzorovou úlohu s tak nesprávným a matoucím číselným zápisem. Děkuji za upřesnění.
Offline
#7 13. 10. 2018 12:43 — Editoval Rumburak (13. 10. 2018 12:52)
Re: Slovní úlohy o pohybu - interpretace
↑ Lokutus:
Zdravím a vyjádřím se k úloze 1.
Především nutno si uvědomit, že slovem "rychlost" je zde míněna rychlost průměrná (jejíž hodnotou je
celková dráha vydělená celkovým časem) a nikoliv rychlost okamžitá, která se během jízdy obecně může
měnit.
Máme zde 2 podmínky:
(1) Ivan urazil na kole trať dlouhou 96 km v čase o 2 hodiny kratším, než původně předpokládal.
(2) Za každou hodinu ujel o 1 km více, než měl původně urazit za 1 h 15 min.
Rozeberme podmínku (1). Označme  skutečnou dobu Ivanovy jízdy (měřeno v hodinách). To znamená,
skutečnou dobu Ivanovy jízdy (měřeno v hodinách). To znamená,
že Ivan jel průměrnou rychlostí  (v km za hod.). Ivan ale předpokládal dobu
(v km za hod.). Ivan ale předpokládal dobu 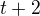 , tedy
, tedy
průměrnou rychlost 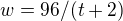 .
.
Rozeberme podmínku (2). Při předpokládané rychlosti  by za 1 h 15 min (což je 5/4 hod.) urazil vzdálenost
by za 1 h 15 min (což je 5/4 hod.) urazil vzdálenost 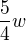 ,
,
při skutečné rychlosti  by za za 1 h urazil vzdálenost
by za za 1 h urazil vzdálenost 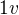 . Podmínka (2) dále říká, že
. Podmínka (2) dále říká, že 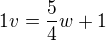 .
.
Celkem tedy dostáváme soustavu tří rovnic
 ,
, 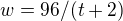 ,
, 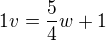
o třech neznámých.
(Úloha mne zaujala a rád jsem si ji zanalysoval - doufám, že jsem nic nepoletl.
Offline