Matematické Fórum

↑ check_drummer:

Ahoj,

myslím, že větu o úplnosti chápeš správně. Zní to jako docela silná podmínka, ale člověk dokáže po chvilce přemýšlení přijít na celou obecnou rodinu příkladů teorií, kdy je splněna. Konkrétně: Kdykoli mám strukturu v nějakém jazyce, můžu uvažovat množinu všech sentencí daného jazyka platných v dané struktuře (). To je zcela zřejmě vždy úplná teorie, jelikož kdykoli mám sentenci, buď je sama součástí té teorie, nebo je součástí teorie její negace.

Odtud je mimo jiné vidět, že ne každá teorie dost silná na to, aby formalizovala aritmetiku, je nutně neúplná - Když třeba vezmu 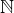jako strukturu v a podívám se na , tak to je určitě úplná teorie a je dost silná na formulování aritmetiky. Čeho se týká Gödelova (první) věta o neúplnosti, jsou rekurzivně spočetné teorie - tj. takové, že je dokáže vypsat nějaký stroj, když mu dáš nekonečně mnoho času. Takže z tohoto pohledu říká např. o teorii , že ji zkrátka "jen" není možné nějak rozumně axiomatizovat, tj. vzít si papír a tužku a napsat si pár axiomů a pár schémat axiomů, ze kterých by už plynul zbytek tvrzení.

Když se na to člověk kouká takto, přijde, mi, že ta věta o neúplnosti stále docela překvapivá je - nejde ani tak o to, že když mám nějaké axiomy popisující aritmetiku, řekněme PA, tak že by je nešlo doplnit na úplnou teorii, ale jde o to, že tato doplnění jsou v jistém smyslu "nepřístupná" (tj. musím tam přidat tak divokou kolekci axiomů, že bych stroji nevysvětlil, jak to dělám).