Matematické Fórum

terezkaaaaa5 · 04. 02. 2015 11:18

Dobrý den, pomůžete mi prosím jak na tento příklad? Potřebovala bych hned počáteční krok. Předem děkuji.

$\lim_{x\to\infty }x\cdot \mathrm{e}^{3x}$

Pavel · 04. 02. 2015 11:28

↑ terezkaaaaa5:

Dosadit za x nekonečno.

terezkaaaaa5 · 04. 02. 2015 11:32

↑ Pavel:

Tak to vyjde $\infty \cdot konstanta$ = nekonečno, že?

A Když bude limita pro mínus nekonečno? :)

Pavel · 04. 02. 2015 11:41

↑ terezkaaaaa5:

Odkud jsi vzala tu konstantu?

Pro limitu v mínus nekonečnu s přepiš součin na podíl s tím, že exponenciála bude ve jmenovateli se záporným exponentem. A pak použij l'hospitalovo pravidlo.

terezkaaaaa5 · 04. 02. 2015 11:42

↑ Pavel:

Pravda, v prvním případě to bude nekonečno * nekonečno. Šlo by to i bez použití L´H pravidla? :)

vlado_bb · 04. 02. 2015 11:46

↑ terezkaaaaa5:Samozrejme. Pre $x>0$ je $e^{3x}>1$ a teda $xe^{3x}>x$ . No a zvysok z definicie limity.

terezkaaaaa5 · 04. 02. 2015 11:48

↑ vlado_bb:

Díky, ale nic moc mě díky tomu nenapadlo. Zvlášť, když x jde k mínus nekonečnu.

terezkaaaaa5 · 04. 02. 2015 12:06

Podle Wolfram Alpha by to mělo vyjít rovno nule. Ale nevím jak k tomu dojít :(

vlado_bb · 04. 02. 2015 12:41

↑ terezkaaaaa5:Aha, minus nekonecno ... Ja som uvazoval o povodnej limite, z prveho prispevku. Ak ide o limitu v minus nekonecne, tak sa asi l'Hospitalovmu pravidlu nevyhneme.

terezkaaaaa5 · 04. 02. 2015 12:45

↑ vlado_bb:

dobře, děkuji.

maver · 04. 02. 2015 15:53

↑ terezkaaaaa5:
není náhodou nekonečno krát nekonečno zakázané?

jelena · 05. 02. 2015 15:12

↑ maver:

Zdravím,

"zakázané" není. Pokud máš na myslí, že to je neurčitý výraz, tak ani to ne, "nekonečno"*"nekonečno" dává v limitě opět nekonečno. To je pro limitu $\lim_{x\to\infty }x\cdot \mathrm{e}^{3x}$ .

Pro limitu 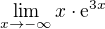$\lim_{x\to-\infty }x\cdot \mathrm{e}^{3x}$ viz debata kolegů (zde už není "nekonečno"*"nekonečno"). Je vidět? Děkuji.

Lotus93

$\frac{x}{e^{-3x}} = |"\frac{inf}{inf}"| = \frac{1}{-3e^{-3x}} = |"\frac{1}{-inf}"| = 0$

Je to správně ? :)

jelena · 06. 02. 2015 00:21

↑ Lotus93:

Zdravím a děkuji, pro 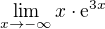$\lim_{x\to-\infty }x\cdot \mathrm{e}^{3x}$ mi vyšlo stejně, akorát nevynechávej, prosím, znaky limity a k čemu jde x, v zápisu \infty dá $\infty$

Lotus93 · 06. 02. 2015 07:37

↑ jelena:
Jo promiň, jsem tu tak 3 dny a pořád jsem se nenaučil se syntaxí.

Matematické Fórum

#1 04. 02. 2015 11:18

Limita funkce

#2 04. 02. 2015 11:28

Re: Limita funkce

#3 04. 02. 2015 11:32

Re: Limita funkce

#4 04. 02. 2015 11:41

Re: Limita funkce

#5 04. 02. 2015 11:42

Re: Limita funkce

#6 04. 02. 2015 11:46

Re: Limita funkce

#7 04. 02. 2015 11:48

Re: Limita funkce

#8 04. 02. 2015 12:06

Re: Limita funkce

#9 04. 02. 2015 12:41

Re: Limita funkce

#10 04. 02. 2015 12:45

Re: Limita funkce

#11 04. 02. 2015 15:53

Re: Limita funkce

#12 05. 02. 2015 15:12

Re: Limita funkce

#13 05. 02. 2015 19:52 — Editoval Lotus93 (05. 02. 2015 20:44)

Re: Limita funkce

#14 06. 02. 2015 00:21

Re: Limita funkce

#15 06. 02. 2015 07:37

Re: Limita funkce

Zápatí