Matematické Fórum

maver · 06. 03. 2015 14:11

U těchto funkcí mám zjistit, zda je mezi nimi lineární kombinace.

$sin^{2}x ,3cos^{2}x, 4$

Vychází nekonečně mnoho řešení (použije se dosazení libovolných x). Úkolem je upřesnit podmínky pro lineární závislost, která platí pro všechna x.

Zde máme v učebnici napsáno, že zvolíme alfa, beta gama koeficienty tak, aby 0=0, a prý odhadem z této situace lze říct (a po ověření i platí), že alfa=12, beta=4, gama=3.

Moje otázka je: je nějaký trik, jak to odhadnu, ty koeficienty?

vulkan66 · 06. 03. 2015 14:36

Ahoj, netriviální lineární kombinace je, pokud dokážu najít 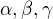$\alpha ,\beta ,\gamma$ tak aby byl alespoň jeden nenulový.
$\alpha \cdot sin^{2}x+\beta \cdot 3cos^{2}x=\gamma \cdot 4$
Podle goniometrické identity je $sin^{2}x+cos^{2}x=1$ a z té se dají jednoduše koeficienty zjistit.

Formol · 06. 03. 2015 14:37

↑ maver:
Ahoj,
předpokládám, že nemáš zjistit, zda "je mezi nimi lineární kombinace", ale máš ověřit, zda je jsou tyto tři funkce lineárně nezávislé.

Trik (pokud to není moc hrdé označení) je v tom, že funkce budeš pokládat za "symboly", ale za symboly, které jde nějak "upravit".
Celé si to nejlépe představíš, když se mechanicky zeptáš, zda existuje netriviální lineární kombinace, která bude nula bez ohledu na x, tj. zda existují reálná čísla taková, že:
$\alpha\sin^2 x + 3\beta\cos^2 x + 4\gamma = 0$

Pak si stačí jen uvědomit, že funkční předpisy nejsou jen symboly, protože:
$\sin^2 x = 1- \cos^2 x$

Tedy vlastně máš
$\alpha(1- \cos^2 x) + 3\beta\cos^2 x + 4\gamma = 0$

A teď jen hledáš koeficienty tak, aby se ti odečetly kosiny a gama si pak zvolíš tak, aby se ti odečetly i konstanty.

Rumburak

↑ maver:

Jeden "trik" mne napadl.

Hledáme všechny uspořádané trojice

(1) $(\alpha, \beta, \gamma)$

takové, aby rovnice

(2) $\alpha\sin^2 x + 3\beta\cos^2 x + 4\gamma = 0$

byla splněna identicky (tj. pro libovolné $x$ ). Jestliže (1) vyhovuje této podmínce,
pak zderivováním rovnice (2) podle $x$ dostáváme

$2 \alpha\sin x \cos x - 6\beta\cos x \sin x = 0$ ,
$(2 \alpha - 6\beta) \sin x \cos x = 0$ ,

pro $x = \frac{\pi}{4}$ je $\sin x \cos x \ne 0$ , takže $2 \alpha - 6\beta = 0$ , tedy $\alpha = 3\beta$ .

Dosazením $x=0$ do (2) dostáváme další rovnici $3\beta + 4\gamma = 0$ , tedy $\gamma = -\frac{3}{4}\beta$ .
Odvodili jsme tedy nutné podmínky na usp. trojici (1). Že jde zároveň o podmínky postačující,
by obecně také potřebovalo důkaz.

Nejlepším trikem je zde ovšem znát identitu $\sin^2 x + \cos^2 x = 1$ .

maver · 09. 03. 2015 12:59

podle toho co tu píšete,
co když si zvolím $\alpha =20$

pak pokud mám splnit podmínku $\alpha - \alpha cos^{2}x +3\beta cos^{2}x+4\gamma =0$
pak
$\alpha +4\gamma =0$
$\alpha = -4\gamma$
$\gamma =-5$

a dál
$-\alpha cos^{2}x+3\beta cos^{2}x=0$
$\alpha cos^{2}x=3\beta cos^{2}x$
$\beta=20/3$

jde to také tak?