Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Kvadratický moment průřezu pro část mezikruží (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 03. 2015 17:53
Kvadratický moment průřezu pro část mezikruží
Ahoj,
Potřeboval bych zjistit kvadratický moment průřezu (modul pruřezů v ohybu) části mezikruží konkrétně se jedná o toto mezikruží:
Předem děkuji za pomoc.
Offline
- (téma jako vyřešené označil(a) Mutak)
#2 12. 03. 2015 12:47 — Editoval FliegenderZirkus (12. 03. 2015 12:48)
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Kvadratický moment průřezu pro část mezikruží
Ahoj,
vůči které ose se má ten moment určit? A musí být výsledek úplně přesný? Ptám se proto, že pokud bychom ten výřez považovali za mezikruhovou výseč, tak půjde výsledek vyjádřit jendoduše pomocí součtů a rozdílů jednoduchých útvarů, pro které jsou hodnoty momentů v tabulkách (nebo se dají snadno odvodit). Jestli ale musíš uvažovat ty hrany řezů skutečně rovnoběžné, tak budeš muset určit hranice pro integraci a sestavit ty integrály z definice kvadratického průřezu. V praxi bude výsledek skoro stejný a nikdo by se tím nezabýval.
Potřebné vzorečky pro ten zjednodušený výpočet jsou tady:
Wikipedia
Offline
#3 13. 03. 2015 09:53
Re: Kvadratický moment průřezu pro část mezikruží
Jednodušší ba to mělo být nejspíš k ose symetrie a nejspíš aji lepší, protože prochází těžištěm. Samozřejmě ten výřez nemusí být rovnoběžný. Zkusím to udělat podle těch vzorečku cos tu posílal. Díky za reakci
Offline
#4 13. 03. 2015 17:38 — Editoval Mutak (13. 03. 2015 17:55)
Re: Kvadratický moment průřezu pro část mezikruží
Kvadratický moment průřezu mezikruží je 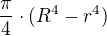 pro mezikruhovou výseč
pro mezikruhovou výseč  (úhel dosazujeme v radiánech). Hledaný kvadratická moment získáme jejích rozdílem
(úhel dosazujeme v radiánech). Hledaný kvadratická moment získáme jejích rozdílem  . Modul průřezu v ohybu je pak
. Modul průřezu v ohybu je pak 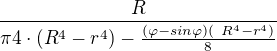
Je to správně?
Offline
#5 13. 03. 2015 20:14 — Editoval FliegenderZirkus (13. 03. 2015 20:14)
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Kvadratický moment průřezu pro část mezikruží
Ahoj,
když budeme nosník ohýbat vůči ose symetrie (tj. na obrázku svislé ose), tak půjde o prostorový (šikmý) ohyb. Nebylo to spíš myšleno tak, že se ohýbá vůči té vodorovné ose? Většinou se totiž myslím ty průřezy kreslí tak orientované, že síly působí seshora, ne zleva nebo zprava. Na každý pád bych řekl, že máš chybu ve výpočtu modulu v ohybu, kde se dělí kvadratický moment vzdáleností krajního vlákna od těžiště -- ne obráceně!
Kdybychom ohýbali vůči té vodorovné ose, tak je potřeba začít výpočtem polohy těžiště a pak použít Steinerovu větu. Taky by bylo potřeba najít nebo odvodit vzoreček na výpočet té výseče pro druhou osu.
Možná budu trochu navádět k lenosti, ale nemůžu nezmínit možnost nechat si všechny podobné veličiny spočítat v CADu, zde např. Autodesk Inventor:
Offline
#6 13. 03. 2015 21:20
Re: Kvadratický moment průřezu pro část mezikruží
Inventor mě nenapadlo použít, ale každopádně pro můj účel postačí. Momenty budu potřebovat pro obě dvě osy, protože to budu uhýbat jak ze strany tak z hora. Děkuji moc za rady hlavně jsem si konečně ujasnil, že se to musí dělit vzdálenosti měl jsem vtom chaos.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Kvadratický moment průřezu pro část mezikruží (TOTO TÉMA JE VYŘEŠENÉ)
