Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lineární závislost vektorů (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 03. 2015 22:26
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Lineární závislost vektorů
Dobrý den, pomůžete mi prosím s tímto příkladem?
Mám zjistit, zda-li jsou lineárně závislé funkce f1 (x) =  a f2 (x) =
a f2 (x) = 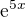 .
.
Vím, že funkce jsou lineárně závislé, pokud  . Ale dál už si rady nevím. Předem díky za pomoc.
. Ale dál už si rady nevím. Předem díky za pomoc.
Offline
- (téma jako vyřešené označil(a) terezkaaaaa5)
#2 07. 03. 2015 22:32
- misaH
- Příspěvky: 13467
Re: Lineární závislost vektorů
↑ terezkaaaaa5:
Podľa mňa tá definícia závislosti dvoch vektorov je nesprávna.
Offline
#3 07. 03. 2015 22:51
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lineární závislost vektorů
↑ misaH:
Je možné, že jsem popletla i toto.
Offline
#4 08. 03. 2015 08:33
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lineární závislost vektorů
Zdravím,
↑ terezkaaaaa5: spíš jsi nedopsala předpoklad ověření. Sestavila jsi lineární kombinaci funkcí  (a položila jsi tuto lineární kombinaci rovnou 0) a "vím, že funkce jsou lineárně závislé, pokud" tato lineární kombinace bude platná pro která
(a položila jsi tuto lineární kombinaci rovnou 0) a "vím, že funkce jsou lineárně závislé, pokud" tato lineární kombinace bude platná pro která  a
a  ? Děkuji.
? Děkuji.
Offline
#5 08. 03. 2015 09:28
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lineární závislost vektorů
↑ jelena:
Že  nebo
nebo  bude nenulové
bude nenulové
Offline
#6 08. 03. 2015 09:29
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lineární závislost vektorů
↑ terezkaaaaa5: ano, přesně tak.
Offline
#7 08. 03. 2015 09:48
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lineární závislost vektorů
↑ jelena:
A jak prosím postupovat dál? :)
Offline
#8 08. 03. 2015 10:24
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lineární závislost vektorů
↑ terezkaaaaa5:
vyřešit rovnici  , nejlépe úpravou na součin po vytknutí
, nejlépe úpravou na součin po vytknutí  .
.
Offline
#9 08. 03. 2015 10:49
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lineární závislost vektorů
Po vytknutí  mi zbude z prvního členu
mi zbude z prvního členu  a z druhého
a z druhého  . Takže
. Takže  ?
?
Moc se mi to nezdá, ale nevím, kde mám chybu.
Offline
#10 08. 03. 2015 11:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lineární závislost vektorů
↑ terezkaaaaa5:
mně se to zdá v pořádku, pokračuješ, že  není nulové pro žádné x, proto dořešíš rovnici
není nulové pro žádné x, proto dořešíš rovnici 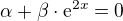 , hledáš parametry
, hledáš parametry  ,
,  .
.
Offline
#11 08. 03. 2015 11:30
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lineární závislost vektorů
↑ jelena:
Díky.  není také nulové pro žádné x. Těch kombinací, kdy
není také nulové pro žádné x. Těch kombinací, kdy 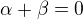 je ale podle mě nespočet.
je ale podle mě nespočet.
Offline
#12 08. 03. 2015 11:55 — Editoval misaH (08. 03. 2015 11:56)
- misaH
- Příspěvky: 13467
Re: Lineární závislost vektorů
↑ terezkaaaaa5:
Ale to nevychádza, že sa má niečomu rovnať alfa+beta.
To by tam musela byť zátvorka.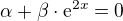

a tak ďalej
Offline
#13 08. 03. 2015 12:08
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lineární závislost vektorů
↑ misaH:
Díky. I tak ale nevím jak dojít ke konkrétním parametrům. Dále vydělím  a vznikne:
a vznikne: 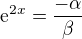 .
.  je vždy kladné, takže aby rovnice platila, musí buď
je vždy kladné, takže aby rovnice platila, musí buď  nebo
nebo  být záporné.
být záporné.
Offline
#14 08. 03. 2015 12:51
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lineární závislost vektorů
↑ terezkaaaaa5:
vydělit můžeš až při nenulové  . Proto začneš se situaci, že
. Proto začneš se situaci, že 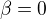 (ještě před dělením), jaká je
(ještě před dělením), jaká je  ? Potom budeš pokračovat pro nenulové
? Potom budeš pokračovat pro nenulové  .
.
Offline
#15 08. 03. 2015 12:57
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lineární závislost vektorů
↑ jelena:
Pokud je  = 0, pak i
= 0, pak i  = 0. Pokud je
= 0. Pokud je  kladné, pak
kladné, pak  je záporné a naopak, pokud je
je záporné a naopak, pokud je  záporné, pak
záporné, pak  je kladné. Je tomu tak?
je kladné. Je tomu tak?
Offline
#16 08. 03. 2015 13:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lineární závislost vektorů
Pokud je
= 0, pak i
= 0.
ano, to jedna platná dvojice  ,
,  .
.
Další povídání není chybné, ale není dost průhledné pro úlohu. Měli bychom prokázat, že jde najít (nebo to nejde) další dvojicí  ,
,  , která bude splňovat rovnost
, která bude splňovat rovnost 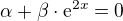 a zároveň nebude závislá na x (jelikož hledáme parametry). Můžeme postupovat obdobně jako při sestavení předpisu lineární funkce ze dvou bodů (to si vybavíš ze ZŠ), zde také: sestavíme 2 rovnice pro různé hodnoty x (např. x=0, x=1), měli bychom mít jen jeden předpis funkce
a zároveň nebude závislá na x (jelikož hledáme parametry). Můžeme postupovat obdobně jako při sestavení předpisu lineární funkce ze dvou bodů (to si vybavíš ze ZŠ), zde také: sestavíme 2 rovnice pro různé hodnoty x (např. x=0, x=1), měli bychom mít jen jeden předpis funkce  (funkční hodnota je pro každý bod nulová).
(funkční hodnota je pro každý bod nulová).
Máme soustavu:
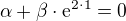
Zkus tuto soustavu vyřešit a udělat závěr, děkuji
Offline
#17 08. 03. 2015 13:50
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lineární závislost vektorů
Z první rovnice mi vyjde 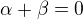 Z této rovnice vyjádřím
Z této rovnice vyjádřím  a dosadím do druhé rovnice. Vytknu
a dosadím do druhé rovnice. Vytknu  a vyjde mi:
a vyjde mi:  . A rovnice je splněna pokud
. A rovnice je splněna pokud 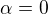
Offline
#18 08. 03. 2015 16:44
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Lineární závislost vektorů
Je to takto správně? A jak dál prosím? :)
Offline
#19 08. 03. 2015 22:20
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lineární závislost vektorů
↑ terezkaaaaa5:
takže vyšlo, že rovnice  je splněna pouze pro nulové
je splněna pouze pro nulové  a
a  (předpokládám, že jsi dořešila i závěr soustavy pro
(předpokládám, že jsi dořešila i závěr soustavy pro 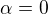 , dosazuješ do
, dosazuješ do  , odkud
, odkud  ). Nenašli jsme žádnou kombinaci koeficientů, aby alespoň jeden byl nenulový. Z toho už můžeš udělat závěr o lineární závislosti zadaných funkcí.
). Nenašli jsme žádnou kombinaci koeficientů, aby alespoň jeden byl nenulový. Z toho už můžeš udělat závěr o lineární závislosti zadaných funkcí.
V pořádku? Děkuji.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lineární závislost vektorů (TOTO TÉMA JE VYŘEŠENÉ)