Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Derivace - konvexnost (TOTO TÉMA JE VYŘEŠENÉ)
#2 26. 03. 2015 18:08
- vulkan66


- Místo: Praha
- Příspěvky: 416
- Škola: ČVUT FJFI - Částicová fyzika
- Pozice: student
- Reputace: 20
Re: Derivace - konvexnost
↑ Danny437:
Největší interval, na kterém je fce konvexní, co jiného by to asi tak bylo..
Vím, jak ovládat vesmír. Tak mi řekněte, proč bych se měl hnát za milionem? -Grigorij Perelman
Offline
#4 26. 03. 2015 19:43 — Editoval vulkan66 (26. 03. 2015 19:44)
- vulkan66


- Místo: Praha
- Příspěvky: 416
- Škola: ČVUT FJFI - Částicová fyzika
- Pozice: student
- Reputace: 20
Re: Derivace - konvexnost
Tu derivaci snad spočítat musíš, ale jestli si tak dobrý, že to dáš z hlavy není problém.
Vím, jak ovládat vesmír. Tak mi řekněte, proč bych se měl hnát za milionem? -Grigorij Perelman
Offline
#5 26. 03. 2015 22:58
Re: Derivace - konvexnost
:-D
Fajn. Tak spočtu derivaci. A potom? Už nic? Protože si řeknu, tak fajn, druhá derivace existuje, a aby byla funkce konvexní, tak musí být větší než 0, tedy v intervalu  ? Nebo se ještě s tou druhou derivací něco dál dělá?
? Nebo se ještě s tou druhou derivací něco dál dělá?
Offline
#6 26. 03. 2015 23:13
Re: Derivace - konvexnost
↑ Danny437:
Označme  , tvým úkolem je vyřešit nerovnici
, tvým úkolem je vyřešit nerovnici  .
.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Derivace - konvexnost (TOTO TÉMA JE VYŘEŠENÉ)

 )? :)
)? :)




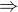
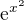 je kladné pro všechna reálná x, stejně jako
je kladné pro všechna reálná x, stejně jako  . Proto pro kladný výsledek stačí, když
. Proto pro kladný výsledek stačí, když  .
.