Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 04. 2015 17:24 — Editoval maver (03. 04. 2015 17:44)
Jádro lineárního zobrazení
Dobrý den,
máme v učebnici 4 řešené příklady, jejímž výsledkům nerozumím:
1)
Já bych napsal, že jádro je KerA=(0,x2,x3)
Ale ve výsledku máme sice, že x1 = 0, a X2,x3 mohou být libovolné,
ale nerozumím zápisu:
2) 
Já bych napsal, že KerA=(0,0,0), ale ve výsledku máme:
KerA=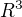
3) A(x)=u u leží v L
Já bych odpověděl, že u=0, ale ve výsledcích je Ker=L
4) A(x)=x+u
Já bych odpověděl, že x+u = 0, takže x= -u, ale ve výsledcích je u=o
Offline
#2 06. 04. 2015 15:26
Re: Jádro lineárního zobrazení
Ahoj ↑ maver:,
Co sa tyka prveho cvicenia, Tvoj zapis riesenia ako aj zapis  je to dobre vyjadrene jadra. Ide len o dva rozlicne zapisy.
je to dobre vyjadrene jadra. Ide len o dva rozlicne zapisy.
2) tu dobra odpoved je 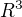 , lebo lubovolny prvok z
, lebo lubovolny prvok z 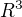 ma nulovy obraz
ma nulovy obraz
3) 4) nie su dostatocne presne vyjadrene, aby ti niekto mohol dat odpoved.
Dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
