Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » lineární dif. rovnice 3. řádu (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 04. 2015 13:40 — Editoval Nia (08. 04. 2015 13:46)
lineární dif. rovnice 3. řádu
ahoj, pořád řeším LDR, tentokrát je to lin. dif. rce 3. řádu, jen bych Vás ráda poprosila o radu, jestli jsou správně vytvořené pravé strany:
tři jednoduché reálné kořeny charakteristické rovnice: 0, 3 a 1
řešení charakteristické rovnice: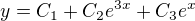
1.část speciální pravé strany: :
: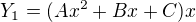
2.část speciální pravé strany (přidala jsem sem x, protože koeficient B odpovídá C1 v řešení char.rovnice - právě tady bych potřebovala radu, protože nevím, jestli uvažuju správně)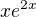 :
: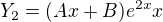
Offline
- (téma jako vyřešené označil(a) Nia)
#4 09. 04. 2015 20:45
Re: lineární dif. rovnice 3. řádu
↑ Nia:
Platí:
Pokud je pravá strana rovna 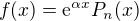 , kde
, kde 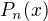 je polynom n-tého stupně, pak partikulární řešení je ve tvaru
je polynom n-tého stupně, pak partikulární řešení je ve tvaru 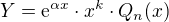 , kde
, kde  je k-násobný kořen charakteristické rovnice a
je k-násobný kořen charakteristické rovnice a 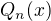 je obecný polynom n-tého stupně.
je obecný polynom n-tého stupně.
Proto 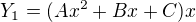 , neboť
, neboť  , 0 je jednonásobný kořen k=1, n=2 .
, 0 je jednonásobný kořen k=1, n=2 .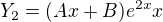 , protože
, protože 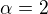 , 2 není kořen k=0, n=1
, 2 není kořen k=0, n=1
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » lineární dif. rovnice 3. řádu (TOTO TÉMA JE VYŘEŠENÉ)


 je správně, 0 je kořenem.
je správně, 0 je kořenem.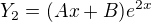 , protože 2 není kořenem.
, protože 2 není kořenem.