Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy ze základní školy
- » Eskalátor - úlohy o pohybu (TOTO TÉMA JE VYŘEŠENÉ)
#1 13. 04. 2015 15:41
Eskalátor - úlohy o pohybu
Zdravím potřeboval bych vysvětlit tento příklad:
7. Při výstupu z metra šel profesor Makos po eskalátoru jedoucím vzhůru a vyšlapal nahoru celkem 20 schodů. Potom spatřil revizora a uvědomil si, že jízdenku z roztržitosti vyhodil dole na nástupišti do koše. Obrátil se tedy a utíkal dolů proti pohybu eskalátoru. Uběhl 140 schodů, ale trvalo mu to dvakrát déle, než cesta nahoru. Lístek z koše šťastně vylovil a když se chtěl vrátit tak zjistil, že se mezitím eskalátor porouchal. Kolik schodů musel vyšlapat nahoru po nepohybujícím se eskalátoru?
Řešení mám, ale nechápu, jak se ty rovnice sestavují:
20 schodů ... t
140 schodů ... 2t
Počet schodů stojícího eskalátoru označíme ... n, pak
n = 20 + x = 140 - 2x (1),
x = 40,
n = 60.
Ale říkám, nechápu, jak sestavit tu rovnici (1), navíc vždyť jsou tam smíchané schody a čas!?
Vysvětlil by mi to někdo, prosím?
Díky.
"Znám dva tisíce způsobů jak nevyrobit žárovku,
potřeboval bych jeden, aby fungovala."
T. A. Edison
Offline
- (téma jako vyřešené označil(a) smajdalf)
#2 13. 04. 2015 17:56
Re: Eskalátor - úlohy o pohybu
↑ smajdalf:
Ahoj,
z jeho pohybu nahoru vyplývá, že za čas t ujede eskalátor dráhu n-20.
z jeho pohybu dolů vyplývá, že eskalátor ujede za čas 2t dráhu 140-n
Proč?
Ze vztahu
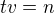 kde n je dráha, vyplývá soustava rovnic:
kde n je dráha, vyplývá soustava rovnic: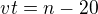
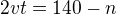
Offline
#3 13. 04. 2015 18:01
Re: Eskalátor - úlohy o pohybu
↑ holyduke:
Díky mockrát !!!
Už to chápu, díky. :-)
"Znám dva tisíce způsobů jak nevyrobit žárovku,
potřeboval bych jeden, aby fungovala."
T. A. Edison
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy ze základní školy
- » Eskalátor - úlohy o pohybu (TOTO TÉMA JE VYŘEŠENÉ)
