Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 04. 2015 16:15
- theveronika1

- Příspěvky: 35
- Škola: SOŠ
- Pozice: student
- Reputace: 0
Posloupnosti
Napište prvních 5 členů posloupnosti a rozhodněte, zda je posloupnost rostoucí nebo klesající a své tvrzení dokažte.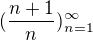
Offline
- (téma jako vyřešené označil(a) jelena)
#3 15. 04. 2015 17:03 — Editoval Al1 (15. 04. 2015 17:10)
Re: Posloupnosti
↑ theveronika1:
Posloupnost je klesající, právě když pro všechna přirozená čísla n platí ( s rostoucím počtem členů klesá jejich hodnota). Pro tvou posloupnost
( s rostoucím počtem členů klesá jejich hodnota). Pro tvou posloupnost . Dokaž závěr dané implikce.
. Dokaž závěr dané implikce.
Offline
#4 15. 04. 2015 20:33
- theveronika1

- Příspěvky: 35
- Škola: SOŠ
- Pozice: student
- Reputace: 0
Re: Posloupnosti
Děkuji všem za pomoc
Offline