Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 04. 2015 16:14
Delitelnost polynomov
Pozravujem,
Nech 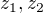 su dve komplexne cisla, a
su dve komplexne cisla, a  polynom z komplexnimi koeficientami taky, ze
polynom z komplexnimi koeficientami taky, ze 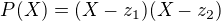 .
.
Urcite 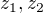 tak aby
tak aby 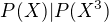 .
.
Upresnite vsetki take polynomy.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 19. 04. 2015 02:14
Re: Delitelnost polynomov
Platí 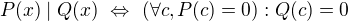 . Má tedy platit (pro jednoduchost označme
. Má tedy platit (pro jednoduchost označme 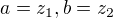 )
) 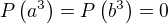 .
.
Dostáváme tak soustavu
jež je symetrická a proto dvojice 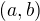 povede ke stejnému polynomu jako
povede ke stejnému polynomu jako 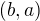 , a kterou upravíme do tvaru
, a kterou upravíme do tvaru
Při pohledu na první tři činitele obou rovnic je jasné, že každá uspořádaná dvojice 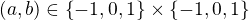 vyhoví. S ohledem na symetrii stačí uvažovat pouze dvojice
vyhoví. S ohledem na symetrii stačí uvažovat pouze dvojice 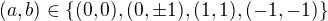 .
.
U další "podsoustavy"
dostáváme krom známých dvojic ještě 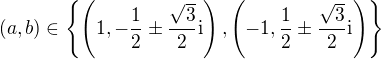 .
.
Nakonec se zbývá podívat na podsoustavu , která po úpravě vede na binomickou rovnici
, která po úpravě vede na binomickou rovnici 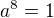 s kořeny tvaru
s kořeny tvaru  a s ohledem na známé dvojice a symetrii stačí uvažovat pouze
a s ohledem na známé dvojice a symetrii stačí uvažovat pouze 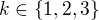 .
.
Všechny vyhovující polynomy jsou tedy tvaru 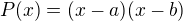 , kde
, kde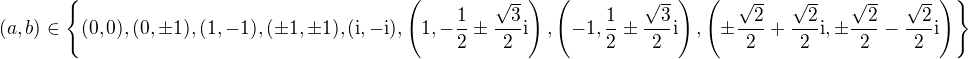
(bereme znaménka pouze na stejné úrovni, tj. např. 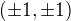 odpovídá pouze dvojicím
odpovídá pouze dvojicím 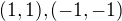 .)
.)
Úloze vyhoví právě 13 různých polynomů.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#3 19. 04. 2015 10:12
Re: Delitelnost polynomov
Ahoj ↑ byk7:,
Rychlo a dobre si to zvladol.
Co sa tyka poslednej otazky, ( ktora je sucast cvicenia) doporucujem pisat polynomy ( ktore su algebricke objekty) z ![kopírovat do textarea $\mathbb{C}[X] $](/mathtex/e9/e9f74a6e367c6dcfec965c4db207fd4e.gif) vo forme ako napr. tu
vo forme ako napr. tu 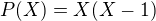 . Pisat X a nie x nam umoznuje tiez okamzite rozlisovat polynom P, a polynomialnu asociovanu funkciu
. Pisat X a nie x nam umoznuje tiez okamzite rozlisovat polynom P, a polynomialnu asociovanu funkciu ![kopírovat do textarea $P: \mathbb{C}[X] \rightarrow \mathbb{C}[X]:x\mapsto P(x)$](/mathtex/0c/0ca2579672bacb82f2df4c004de13502.gif) .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
