Matematické Fórum

jurajjj · 19. 04. 2015 09:52

Jak dokážu, že tato limita vyjde $-\infty$

//forum.matweb.cz/upload3/img/2015-04/29875_limit2.png

jinsun · 19. 04. 2015 10:45

↑ jurajjj:
mám za to, že stačí jenom dosadit, ale nejsem si 100% jistý
P.S. hodně štěstí v pondělí :)

jurajjj · 19. 04. 2015 10:50

Po dosazení vyjde -1/0 což není $-\infty$

Al1 · 19. 04. 2015 11:04

↑ jurajjj:

$\lim_{[x;1]\to [-1;1]}\frac {-1}{|3+x-2|} =\lim_{x\to -1}\frac {-1}{|x+1|}=-\infty$ ,
neboť ve jmenovateli pokud zvolíme jednostranné limity k (-1) zprava a zleva obdržíme vždy číslo kladné o maličko větší než nula. Dělíme tedy (-1) maličko kladným číslem a výsledek je $-\infty$

Stýv · 19. 04. 2015 11:05

↑ jurajjj: jaký je definiční obor té fce?

jurajjj · 19. 04. 2015 11:36

↑ Al1:
Díky, takto jsem to chtěl vidět.

Stýv · 19. 04. 2015 12:44

↑ Al1: toto ovšem není správné řešení

jurajjj · 19. 04. 2015 14:51

↑ Stýv:Co je tedy správné řešení?

Al1 · 20. 04. 2015 09:07

Opravuji

Výpočtem dvojnásobných limit

$\lim_{[x;1]\to [-1;1]}\frac {-1}{|3+x-2|} =\lim_{x\to -1}\frac {-1}{|x+1|}=-\infty$

$\lim_{[-1;y]\to [-1;1]}\frac {-1}{|3-1-2y|} =\lim_{y\to1}\frac {-1}{|2-2y|}=-\infty$

Toto ještě nemusí vést k závěru, že dvojná limita existuje.

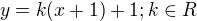Přibližujeme-li se k bodu $[-1;1]$ po přímkách $PP_{0}; P[x;y]; P_{0}[-1;1]$ , které mají rovnic $y=k(x+1)+1; k\in R$ , dostáváme

$\lim_{[x;y]\to [-1;1] y=k(x+1)+1}\frac {-1}{|3+x-2y|}=\lim_{[x;y]\to[-1;1]}\frac{-1}{|3+x-2\big(k(x+1)+1\big)}=\lim_{x\to-1}\frac{-1}{|(1-2k)(x+1)|}$

Limita závisí na k, proto neexistuje.

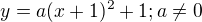Přibližujeme-li se k bodu $[-1;1]$ po svazku parabol s vrcholem $[-1;1]$ , které mají rovnici $y=a(x+1)^{2}+1; a\neq0$ , dostáváme

$\lim_{[x;y]\to [-1;1] y=ax^{2}+2ax+2a+1}\frac {-1}{|3+x-2y|}=\lim_{[x;y]\to[-1;1]}\frac{-1}{|3+x-2(ax^{2}+2ax+2a+1)|}=\lim_{x\to-1}\frac{-1}{|-a|}$

Limita neexistuje.

Odkaz