Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 05. 2009 19:22
usměrňování zlomků
Dobrý den prosím o kontrolu tohoto příkladu:
Pod odmocninou5 + 3*pod odmocninou7/celé lomeno pod odmocninou7 - pod odmocninou 5
Mě vyšlo 2 * pod odmocninou 35 + 26. Ve výsledcích je 2 * pod odmocninou 35+13. Prosím o kontrolní výpočet co je správně.
Offline
- (téma jako nevyřešené označil(a) jelena)
#7 06. 05. 2009 16:53
Re: usměrňování zlomků
↑ lenisek:
Díky :))
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#11 26. 05. 2010 21:02 — Editoval jelena (26. 05. 2010 21:32)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: usměrňování zlomků
↑ tomec:
Zdravím, něco takového:
EDIT: opravila jsem znaménko v čitateli na závěr.
klepní si na můj zápis, řenese se do zprávy a můžeš pokračovat, provedla bych na úvod toto: 
a užitežný vzorec 2.3
Příště prosím nové téma, děkuji.
Offline
#16 27. 05. 2010 09:35 — Editoval frank_horrigan (27. 05. 2010 09:38)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: usměrňování zlomků
↑ doomed:
Založ si vlastní thread, pak se ti na to rádi podíváme :)
EDIT: jestli ti stačí jenom ten výraz, tak je to 
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#18 27. 05. 2010 10:02
Re: usměrňování zlomků
↑ zdenek1: a kam se poděla ta mínus dvojka ve jmenovateli, resp. mínus jednička v čitateli?
Offline
#19 27. 05. 2010 10:11 — Editoval Cheop (27. 05. 2010 12:51)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: usměrňování zlomků
↑ doomed:
Možný výsledek je i tento: (jinou úpravou) jenom toto
jenom toto  je roznásobeno a necháno pod odmocninou.
je roznásobeno a necháno pod odmocninou.
Možné úpravy tedy jsou:
1) 
2) 
PS: Můžeš si vybrat, která se Ti líbí víc
Nikdo není dokonalý
Offline
#24 27. 05. 2010 12:31
Re: usměrňování zlomků
Offline
#25 27. 05. 2010 13:43
Re: usměrňování zlomků
Sypu si popel na hlavu, samozřejmě máte pravdu, špatně jsem napsal zadání, má tam být  Ale stejně mi zůstává záhodou, jak vhodně zvolit ten výraz, kterým rozšiřuju čitatele a jmenovatele. V tomhle případě už je mi to jasný, ale trvalo mi to. Existuje nějaké pravidlo?
Ale stejně mi zůstává záhodou, jak vhodně zvolit ten výraz, kterým rozšiřuju čitatele a jmenovatele. V tomhle případě už je mi to jasný, ale trvalo mi to. Existuje nějaké pravidlo?
Offline











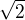
 na
na 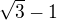
 a pak ho ještě při dalších úpravách v čitateli umocním a odmocním, dostanu jeho absolutní hodnotu a ne jeho skutečnou hodnout.
a pak ho ještě při dalších úpravách v čitateli umocním a odmocním, dostanu jeho absolutní hodnotu a ne jeho skutečnou hodnout.
 ?
?