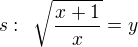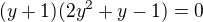Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Řešení rovnice metodou substituce (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 04. 2015 16:44
Řešení rovnice metodou substituce
Ahoj,
počítal jsem si nějaké příklady z Petákové, ale bohužel jsem se zasekl u příklady ze strany 16/27f. 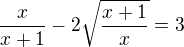
Použil jsem substituci  a postupnou úpravou jsem se dostal k rovnici
a postupnou úpravou jsem se dostal k rovnici  .
.
Ta se mi jednak těžce řeší, ale také se mi nezdá jako ten správný postup.
Kde dělám chybu?
Díky moc!
Offline
- (téma jako vyřešené označil(a) gadgetka)
#2 26. 04. 2015 17:04 — Editoval vulkan66 (26. 04. 2015 17:06)
- vulkan66


- Místo: Praha
- Příspěvky: 416
- Škola: ČVUT FJFI - Částicová fyzika
- Pozice: student
- Reputace: 20
Re: Řešení rovnice metodou substituce
↑ moonek:
Ahoj, ty příklady jsou dělané tak, aby šel jeden kořen snadno uhodnout. Zkus dosadit -1,1.
Když máš jeden kořen, kvadratickou rovnici spočítáš snadno.
Vím, jak ovládat vesmír. Tak mi řekněte, proč bych se měl hnát za milionem? -Grigorij Perelman
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Řešení rovnice metodou substituce (TOTO TÉMA JE VYŘEŠENÉ)