Matematické Fórum

Andrejka3 · 11. 05. 2015 23:42

Ahoj.
Jak dokážu ekvivalenci Goldbachovy hypotézy a následujícího:
T: Je-li 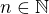$n\in\mathbb{N}$ a $3\leq n$ , pak $n$ je prvočíslem nebo součtem dvou prvočísel nebo součtem tří prvočísel?

Implikace Goldbach (G) implikuje T, je mi jasná.

Přitom vím tohle:

(G): $n$ větší nebo rovno šesti, pak je součtem tří prvočísel.
G_S : $n$ větší nebo rovno šesti a sudé, pak je součtem tří prvočísel.
G_L : $n$ větší nebo rovno šesti a liché, pak je součtem tří prvočísel.
Euler (E): $n$ větší nebo rovno čtyřem a sudé, pak je součtem dvou prvočísel.

Následující jsou ekvivalentní: G, G_S, E.

Zkusila jsem dokázat T implikuje G_S: ať $6\leq n$ . Pak $n$ neni prvocislo. Je-li součtem tří prvočísel, není co řešit. Pokud je součtem dvou prvočísel, pak jsou obě tato prvočísla lichá. Tím končím. To nestačí. Prosím o radu.

Brano · 12. 05. 2015 16:17

a ako sa dokaze ekvivalencia G a E? lebo tam by som asi hladal inspiraciu

Andrejka3 · 12. 05. 2015 16:33

↑ Brano:
Osobně mám podezření, že se jedná o chybičku v textu.

Ekvivalence G a E.

Matematické Fórum

#1 11. 05. 2015 23:42

Goldbach conjecture

#2 12. 05. 2015 16:17

Re: Goldbach conjecture

#3 12. 05. 2015 16:33

Re: Goldbach conjecture

Zápatí