Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 29. 05. 2015 13:18
- Eratosthenes
- Příspěvky: 2593
- Reputace: 132
Re: Monotonie reálné funkce
ahoj ↑ Bati:,
zkusil bych zderivovat a dokázat, že derivace je záporná. Zdá se mi, že by to mohlo jít.
Budoucnost patří aluminiu.
Offline
#4 30. 05. 2015 12:51
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Monotonie reálné funkce
Zdravím,
je celkem drzost z mé strany se zapojit do vaši debaty, ↑ Eratosthenes:, ↑ Bati: :-)
↑ Bati: pokud tuto otázku pokládáš, tak předpokládám, že tradiční postupy vyšetření monotonie nešlo uplatnit (?). Pomůže uvažovat, že máme součin funkcí, obě jsou v nekonečnu definovány, obě však mají v nekonečnu limity a jsou omezeny (podrobně si to určitě dovedete popsat). Obě nabývají kladných hodnot a součin (tedy samotná f(x)) má asymptotu 0. Tedy má vývoj, že f(x) klesá v kladných hodnotách k 0.
Není to však důkaz, jen popis (a také pokus o oživení tématu). Děkuji.
Offline
#5 30. 05. 2015 13:16 — Editoval jarrro (30. 05. 2015 13:19)
Re: Monotonie reálné funkce
↑ jelena: to nestačí. ak má kladná funkcia asymptotu xovú os ešte nemusí klesať na okolí nekonečna
napríklad  . ľubovoľná kladná funkcia s nulovou limitou v nekonečne má za asymptotu xovú os
. ľubovoľná kladná funkcia s nulovou limitou v nekonečne má za asymptotu xovú os
ak som teda niečo neprehliadol
MATH IS THE BEST!!!
Offline
#6 30. 05. 2015 13:42
Re: Monotonie reálné funkce
Ahoj, tak přidám jednu nekorektní blbost:
složím to zvnitřku s inverzí ( ), takže místo
), takže místo 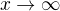 budu mít
budu mít  . Dostanu tohle
. Dostanu tohle![kopírovat do textarea $\frac{e^y-1}{y}\big[\sqrt{1+y}-\sqrt{1+4y^2} \big]$](/mathtex/0e/0e129322ca99b642639313819a2ca4a2.gif) . Teď možná Taylor v nule, člen po členu (promiň matematiko) a nechám to jen do prvního řádu.
. Teď možná Taylor v nule, člen po členu (promiň matematiko) a nechám to jen do prvního řádu. je co mi zůstane a interpretuju to takhle: když jsem hodně blízko nuly a posunu se kousek doprava, tak se mi hodnota o trochu zvětší. Což snad znamená, že původní fce byla klesající.
je co mi zůstane a interpretuju to takhle: když jsem hodně blízko nuly a posunu se kousek doprava, tak se mi hodnota o trochu zvětší. Což snad znamená, že původní fce byla klesající.
What does a drowning number theorist say?
'log log log log ...'
Offline
#7 30. 05. 2015 18:22
Re: Monotonie reálné funkce
Ahoj.
↑ jelena:
Jako drzost to rozhodně neberu, téma stálo. Máš pravdu, že vyšetření monotonie pomocí derivace mi nešlo a ↑ Eratosthenes: zřejmě taky neuspěl. Taky by stačilo dokázat konvexitu apod., ale tím se to, zdá se, nezjednodušuje. Díky za tvůj nápad, nicméně nestačí, jak správně upozornil ↑ jarrro:. Je třeba nějak dokázat, že to "neosciluje".
↑ Andrejka3:
Přesun do nuly je OK, ale poslední úvaha má problém v tom, že když  , tak z toho neplyne, že
, tak z toho neplyne, že  je v okolí nuly rostoucí, viz např. fce
je v okolí nuly rostoucí, viz např. fce  . Jde vlastně asi o stejný problém jako u návrhu ↑ jelena:.
. Jde vlastně asi o stejný problém jako u návrhu ↑ jelena:.
Díky všem za snahu.
Offline
#9 30. 05. 2015 21:07
Re: Monotonie reálné funkce
Ahoj,
puvodne se jedna o muj problem. Od pana vyucijiciho jsem dostal odpoved, ze je potreba spocitat limitu: derivace funkce vydelena vhodnou mocninou - v tomto pripade x^2. Limita (pokud se nepletu) vychazi -1/2 a tedy funkce je klesajici.
Mohl by nekdo vysvetlit, jak tento postup funguje a jak zjistim vhodnou funkci pro deleni? Dekuji.
Offline
#10 30. 05. 2015 22:23
- Eratosthenes
- Příspěvky: 2593
- Reputace: 132
Re: Monotonie reálné funkce
ahoj ↑ karim11:,
tak to se budeš muset zeptat svého vyučujícího - o něčem takovém jsem v životě neslyšel. A zdá se mi to divné. Pokud jsem něco nepřehlédl, limita té derivace - předpokládám pro x -> nekonečno - mi vychází nula, i když není derivace vydělená. Tím spíš je to nula, když ji budu dělit nějakou mocninou x...
Budoucnost patří aluminiu.
Offline
#12 30. 05. 2015 22:31 — Editoval Bati (30. 05. 2015 22:45)
Re: Monotonie reálné funkce
↑ byk7:
Tady ale přece nejde o klasickou exponencielu, ale o fci  , která se pro velká x chová jako
, která se pro velká x chová jako  , tedy "polynom".
, tedy "polynom".
Ta nerovnost je zajímavá, ale nevidím hned, jak to z ní dostat.
↑ karim11:
Ano, to funguje:-) Akorát ta mocnina je  . Platí
. Platí  .
.
To znamená, že existuje  tak, že
tak, že  pro všechna
pro všechna  , ale
, ale  je vždycky kladné, takže nutně
je vždycky kladné, takže nutně  pro každé
pro každé  .
.
Ta mocnina jde uhodnout, když si člověk napíše tu derivaci. U toho jejího prvního členu je celkem evidentní, že by se měl násobit  , aby vyšla limita vlastní (to je pro ten trik důležité). Ten druhý člen pak vyjde 0 shodou okolností.
, aby vyšla limita vlastní (to je pro ten trik důležité). Ten druhý člen pak vyjde 0 shodou okolností.
Překvapuje mě, že jsem se s takovou jednoduchou fintou ještě nesetkal..
Edit: Když o tom tak přemýšlím, stačilo by vzít dostatečně velkou mocninu, která to po vynásobení "převálcuje" a kouknout se, jestli vyjde plus nebo mínus nekonečno (a jestli limita existuje, samozřejmě). Tím válcováním myslím to, že růst té mocniny převáží konvergenci té derivace k nule.
Offline
#13 31. 05. 2015 10:25 — Editoval jarrro (31. 05. 2015 10:29)
Re: Monotonie reálné funkce
je to vyriešené, ale chcem sa len uistiť či mi niečo neušlo
podľa mňa sa podobnou úvahou dá ukázať, že ak pre funkciu f existuje taká funkcia g, že
tak je funkcia f na okolí nekonečna klesajúca
pričom beriem aj nekonečno ako viac ako nula a mínus nekonečno ako menej ako nula
je to tak?
MATH IS THE BEST!!!
Offline
#16 31. 05. 2015 15:29
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Monotonie reálné funkce
Zdravím,
↑ Bati:
Je třeba nějak dokázat, že to "neosciluje".
to jsem zběžně odhadla z vlastností funkcí v součinu (jak jsem psala, že podrobně určitě doplníte, funkce nejsou nepřehledné). Ale obecné (narychlo nic nemám) - můžeme očekávat oscilaci, pokud máme součin 2 monotonních funkcí stejného znaménka, ovšem s "opačnou" monotonii - jedna klesá, druhá roste? Nějaký příklad (zatím máte jen s užitím periodických funkcí)?
↑ příspěvek 12:, ↑ Bati: děkuji, určitě to vidím prvně - lze postup zobecnit na hledání znaménka "obtížně vyšetřitelného výrazu" (v nekonečnu)?
Děkuji, nehoří + dotazy od Jarrro.
Offline
#17 31. 05. 2015 19:17 — Editoval Bati (31. 05. 2015 20:34)
Re: Monotonie reálné funkce
↑ jarrro: ?
?
↯ :  .
.  .
. ↯ □
↯ □
Takže mně se zdá, že to stačí, co myslíš?
↑ jelena:
jelena napsal(a):
Ale obecné (narychlo nic nemám) - můžeme očekávat oscilaci, pokud máme součin 2 monotonních funkcí stejného znaménka, ovšem s "opačnou" monotonii - jedna klesá, druhá roste? Nějaký příklad (zatím máte jen s užitím periodických funkcí)?
Vím, co máš na mysli, taky jsem uvažoval tímto způsobem a přišlo mi intuitivně zřejmé, že taková funkce musí být monotónní, viz moje úvodní reakce ↑↑ Bati:. Zdá se mi ale, že taková intuice je spíš způsobena tím, že se v "učebnicových" příkladech nesetkáváme s dostatečně zajímavými funkcemi a naše představivost je tím pádem omezena zhruba na nějakou kombinaci mocnin, exp a sin a tím to hasne. Myslím, že abychom mohli formalizovat tuhle intuici, museli bychom dokázat tvrzení typu
"Rovnice  , kde
, kde  je nějaká racionální funkce svých argumentů (navíc s odmocninami), má konečnou množinu řešení."
je nějaká racionální funkce svých argumentů (navíc s odmocninami), má konečnou množinu řešení."
A to tedy opravdu nevím jak bych dokazoval (už pro obyčejnou racionální funkci to dá docela zabrat) i když opět by se asi dalo řict, že "to je vidět". Ale je samozřejmě možné, že to jde jednodušeji, nevím.
Jinak "oscilace" lze samozřejmě zařídit jinak, než pomocí gon. funkcí, např. ![kopírovat do textarea $(-1)^{[x]}(2x-2[x]-1)$](/mathtex/4b/4bcb2b70ce9989a9b16911fb4099bc65.gif) , kde
, kde ![kopírovat do textarea $[x]$](/mathtex/21/21271f70d45cc2a593fb2a4b47a16998.gif) je dolní celá část. Vím, že to nemá derivace atd atd. ale snad nemusím předvádět, že takové funkce lze najít.
je dolní celá část. Vím, že to nemá derivace atd atd. ale snad nemusím předvádět, že takové funkce lze najít.
Hladší funkce, co vypadá z dálky jako sinus : ![kopírovat do textarea $(-1)^{[\frac{x}{\pi}]}(1-(\tfrac{2x}{\pi}-2[\tfrac{x}{\pi}]-1)^2)$](/mathtex/4d/4d4cc628ef324c5fc5abb00a21c682b1.gif) .
.
Offline
#18 01. 06. 2015 09:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Monotonie reálné funkce
Zdravím,
↑ Bati: děkuji, ale taková navržená funkce nesplňuje požadavek monotonnosti - je tak? Děkuji, ani trochu nehoří :-)
Jinak hodně škoda, že v odkazovaném tématu, odkud pramení problém, se více nezapojil kolega Marian (jen skrytým příspěvkem). Snad se ještě podívá.
Offline
#20 01. 06. 2015 10:56
Re: Monotonie reálné funkce
Ahoj.
↑ jelena:
To není, ale to už se dá snadno zařídit přenásobením s jinou funkcí, viz ↑ jarrro:.
↑ Rumburak:
Viz ↑ Andrejka3:. Vyřešeno zde ↑ Bati:.
Offline
#21 02. 06. 2015 20:53
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Monotonie reálné funkce
↑ Bati:
děkuji, spíš jsem očekávala nějaký "školsky" vypadající příklad, který by se najednou zjevil jako oscilující (z vašich s Jarrro příkladů je to vidět rovnou). Souhlasím, že jen odhad o součinu "opačně monotonních" a omezených funkcí není důkaz.
Offline

 je v jistém okolí nekonečna klesající?
je v jistém okolí nekonečna klesající? .
. je
je  , ale to asi k ničemu nebude.
, ale to asi k ničemu nebude.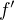 existuje, stačí prostě odhadnout nějakým epsilonem>0 - máme ostré nerovnosti.
existuje, stačí prostě odhadnout nějakým epsilonem>0 - máme ostré nerovnosti.
 a pod.
a pod.