Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 06. 2015 00:02
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Orientovaný plošný integrál
Zdravím tak trochu tápu nad tím, jak se určuje orientace normály u plošných integrálů.
Dejme tomu mám příklad
Spočtěte plošný integrál 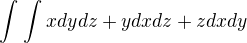 kde
kde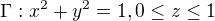
Normála míří ven.
Tudíž mám udělám veektorový součin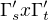 a dostanu vektor
a dostanu vektor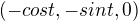 Jak poznám zda je tento vektor souhlasně orientovaný s normálou nebo není?
Jak poznám zda je tento vektor souhlasně orientovaný s normálou nebo není?
Offline
#3 01. 06. 2015 00:31
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Re: Orientovaný plošný integrál
↑ Brano:
Takže zjistím že v počátku souřadného sysstému má tento vektor 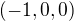 no a vždyť tenhle vektor je jakoby ve spodní podstavě válce ? Chápu to takhle dobře? Protože mi přijde, že jak teď určit jestli míří do nebo ven když je přímo v té ploše. Nebo jsem ten vektorový součin spočítal špatně ?
no a vždyť tenhle vektor je jakoby ve spodní podstavě válce ? Chápu to takhle dobře? Protože mi přijde, že jak teď určit jestli míří do nebo ven když je přímo v té ploše. Nebo jsem ten vektorový součin spočítal špatně ?
Offline
#4 02. 06. 2015 10:09
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Re: Orientovaný plošný integrál
Můžu se tedy zeptat jak orientovat ty plochy aby byly souhlasně orientovány ?
Offline
#5 03. 06. 2015 21:08
Re: Orientovaný plošný integrál
no lenze ten vektor si musis posadit do bodu v ktorom ho pocitas
parametrom 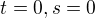 zodpoveda predpokladam bod
zodpoveda predpokladam bod 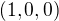 (totizto si nenapisal parametrizaciu co si zvolil, tak len hadam) - a tam zasadis ten vektor - t.j. to bude orientovana usecka z
(totizto si nenapisal parametrizaciu co si zvolil, tak len hadam) - a tam zasadis ten vektor - t.j. to bude orientovana usecka z 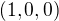 do
do 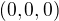 cize smeruje dnu
cize smeruje dnu
Offline

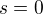 a
a  si uvedom v akom bode plochy sedi ten vektor a aky je a uvidis ci smeruje dnu alebo von.
si uvedom v akom bode plochy sedi ten vektor a aky je a uvidis ci smeruje dnu alebo von.