Matematické Fórum

rss · 15. 06. 2015 12:04 — Editoval rss (16. 06. 2015 07:51)

Dobrý deň. Pomôžete s týmto príkladom?:

2 hmotné body sa gravitačne priťahujú. Vyjadrite okamžitú vzdialenosť medzi bodmi ako funkciu času, hmotností bodov, gravitačnej konštanty a ich počiatočnej vzdialenosti. Počiatočná rýchlosť je nulová.

rss · 15. 06. 2015 12:09 — Editoval rss (16. 06. 2015 09:03)

Uvažoval som tieto vzorce:
G = k . M / r^2
g = k . m / r^2
S = 0,5 . G . t^2
s = 0,5 . g . t^2
r = R - S - s

Legenda:
G - gravitačné zrýchlenie pre 1. bod
g - gravitačné zrýchlenie pre 2. bod
m - hmotnosť 1. bodu
M - hmotnosť 2. bodu
k - gravitačná konštanta
r - okamžitá vzdialenosť bodov
R - počiatočná vzdialenosť bodov
S - dráha ktorú prejde 1. bod k spoločnému ťažisku
s - dráha ktorú prejde 2. bod k spoločnému ťažisku

r = R - S - s
r = R - 0,5.t^2.(G + g)
r = R - 0,5.t^2.k.(M + m)/r^2
r^3 = R.r^2 - 0,5.t^2.k.(M + m)
r^3 - R.r^2 + 0,5.t^2.k.(M + m) = 0

Môžete vyriešiť kubickú rovnicu?
x^3 - b.x^2 + d = 0
Napríklad takto: https://cs.wikipedia.org/wiki/Cardanovy_vzorce ?
Dá sa to riešiť jednoduchšie?

pietro · 15. 06. 2015 17:24 — Editoval pietro (15. 06. 2015 17:26)

↑ rss: Ahoj, ak budú m1=m2=m a počiat rýchlosť nulová

potom a*m=k*m*m/r*r ==> a=r"(t)=b/r2
alebo pre wolfram

x''(t)*x(t)^2 =b, x(0)=r0, x'(0)=0

Odkaz

čo sa mu Wolfra-mu akosi nechce riešiť. :-(

(niekedy áno, niekedy nie)

rughar · 15. 06. 2015 17:39 — Editoval rughar (15. 06. 2015 17:40)

Jde to řešit pomocí difereniálních rovnic, nejlépe vyjít z rovnic pro celkovou energii a hybnost

$m_1 v_1 + m_2 v_2 = {\rm konst}\\ \frac{1}{2}m_1 v_1 + \frac{1}{2}m_2 v_2 -G \frac{m_1m_2}{r}= {\rm konst}$

Ale lepší je možná řešit situaci drobným trikem. Tam diferenciální rovnice není potřeba. Nasměruju, ale řešení nechám na vás :)

1. Krok: Druhý a třetí Keplerův zákon (Odkaz)
2. Krok: Úsečka o délce '2a' je speciální případ elispy s hlavní poloosou délky 'a'
3. Krok: Zavedení redukované hmotnosti: Při vzájemném gravitačním působení dvou těles lze pro každé těleso říci, že jeho pohyb odpovídá pohybu kolem statického hmotného bodu o hmotnosti 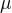$\mu$ umístěném v těžišti soustavy.

$\mu =\frac{m_1m_2}{m_1+m_2}$

rss · 16. 06. 2015 07:55 — Editoval rss (16. 06. 2015 08:00)

rughar napsal(a):
Jde to řešit pomocí difereniálních rovnic, nejlépe vyjít z rovnic pro celkovou energii a hybnost

$m_1 v_1 + m_2 v_2 = {\rm konst}\\ \frac{1}{2}m_1 v_1 + \frac{1}{2}m_2 v_2 -G \frac{m_1m_2}{r}= {\rm konst}$

Prečo je súčet hybností konštantný? Rýchlosť oboch bodov sa zväčšuje. V druhej rovnici neviem čo je G. Je dobré písať legendu k rovniciam.

rughar napsal(a):
Ale lepší je možná řešit situaci drobným trikem. Tam diferenciální rovnice není potřeba. Nasměruju, ale řešení nechám na vás :)

1. Krok: Druhý a třetí Keplerův zákon (Odkaz)
2. Krok: Úsečka o délce '2a' je speciální případ elispy s hlavní poloosou délky 'a'
3. Krok: Zavedení redukované hmotnosti: Při vzájemném gravitačním působení dvou těles lze pro každé těleso říci, že jeho pohyb odpovídá pohybu kolem statického hmotného bodu o hmotnosti $\mu$ umístěném v těžišti soustavy.

$\mu =\frac{m_1m_2}{m_1+m_2}$

Keplerove zákony nechcem použiť, pretože ich chcem dokázať alebo vyvrátiť.

rss · 16. 06. 2015 09:06 — Editoval rss (16. 06. 2015 10:02)

pietro napsal(a):
Ahoj, ak budú m1=m2=m a počiat rýchlosť nulová

potom a*m=k*m*m/r*r ==> a=r"(t)=b/r2

Potrebujem všeobecné riešenie pre rôzne hmotnosti.

pietro napsal(a):
alebo pre wolfram

x''(t)*x(t)^2 =b, x(0)=r0, x'(0)=0

Odkaz

čo sa mu Wolfra-mu akosi nechce riešiť. :-(

(niekedy áno, niekedy nie)

Nerozumiem tomu čo spravil Wolfram. Potrebujem výsledok r = f(t, R, k, M, m)

Prítomnosť imaginárnej zložky znamená že pôsobí aj rotácia?

pietro · 16. 06. 2015 21:32

↑ rss: Aspoň akási grafická predstava , odhad, ako by mala vyzerať trajektória

v polohočase.

Autor skryl část textu. Zobrazit/skrýt!

pietro · 16. 06. 2015 23:01

↑ rss: zatiaľ len nespojité riešenie

Autor skryl část textu. Zobrazit/skrýt!

Brzls · 17. 06. 2015 14:56

↑ rughar:
Není mi jasné, jak keplerovy zákony poslouží k sestavení funkční závislosti vzdálenosti na čase. Na určení doby srážky ok, ale na popsání celé trajektorie to nevím jak.

↑ rss:
Takovýto postup je zcela mimo
↑ rss:
Hybnost je vektorová veličina, to že velikosti hybností rostou, neznamená že se jejich vektorový součet mění.
Na Keplerovy zákony ti stačí zachování momentu hybnosti, zachování energie a nějaká elementární znalost geometrie.

K řešení: Nějakou expicitní formu se asi najít nepodaří, nicméně sestavit rovnice k řešení problém není. rughar to už v podstatě udělal, já jen ukážu, že to jde i jinak. A dokonce to vede i na rovnici, kterou jste již zkoušeli dát do wolframu

Gravitační zákon:
x1 a x2 jsou souřadnice těles s hnotností m1 a m2.

$m_{1}\frac{\mathrm{d} ^{2}x_{1}}{\mathrm{d}t^{2} }=Gm_{1}m_{2}\frac{1}{(x_{1}-x_{2})^{2}}$
$m_{2}\frac{\mathrm{d} ^{2}x_{2}}{\mathrm{d}t^{2} }=-Gm_{1}m_{2}\frac{1}{(x_{1}-x_{2})^{2}}$

1. Sečtením rovnic, a následnou triviální integrací obdržíme rovnici $m_{1}x_{1}+m_{2}x_{2}=0$
2. Když první vydělíme m1 a druhou m2, a poté od sebe odečtem, obrdžíme rovnici

$\frac{\mathrm{d} ^{2}(x_{1}-x_{2})}{\mathrm{d}t^{2} }=G(m_{1}+m_{2})\frac{1}{(x_{1}-x_{2})^{2}}$

substitucí obdržíme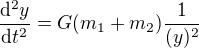
$\frac{\mathrm{d} ^{2}y}{\mathrm{d}t^{2} }=G(m_{1}+m_{2})\frac{1}{(y)^{2}}$

funkce y je vlastně to co nás zajímá (až teď jsem si uvědomil, že nehledáme i jednotlivé funkce x1 a x2). Takže jsme dostali naprosto stejnou dif. rovnici i pro různé hmotnosti.

rughar · 18. 06. 2015 17:01

↑ Brzls:

Doufal jsem v parametrizaci polohy podle obsahu plochy, kterou teleso urazilo v elipticke draze, odkud bychom pak jen presli na degenerovany pripad. Je ale pravda, ze to vypada sloziteji. Nicmene stale bych rekl, ze reseni by v tomto pripade mohlo v pohode projit :). Vzhledem k tomu, jak vypada vysledek, bych tomu dost veril.

Ale nakonec je stejne nejlepší cesta asi pres diferencialni rovnice. Skoncili jsme tedy u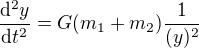

$\frac{\mathrm{d} ^{2}y}{\mathrm{d}t^{2} }=G(m_{1}+m_{2})\frac{1}{(y)^{2}}$

Dovolim si to rozvest. Naleznu integral pohybu, coz je

$\frac{1}{2}\left(\frac{\mathrm{d}y}{\mathrm{d}t }\right)^2 = \frac{G(m_1+m_2)}{y} - \frac{G(m_1+m_2)}{y_0}$

, kde y0 je počáteční vzdálenost. Výpočet vede na integrál

$\int_{y_0}^{y_1} \frac{1}{\sqrt{\frac{\alpha}{y} - \frac{\alpha}{y_0}}} {\rm d} y =- t$

přičemž

$\alpha \equiv 2G(m_1+m_2)$ .

(pozn.: minusko u "t" si dovolim okomentovat na konci). Pokračujeme výpočtem výše uvedného integrálu. Tím získáme implicitní vyjádření mezi hodnotami y a t. Pokračujme s analýzou posledího integrálu. Zavedeme jednoduchou substituci

$y = q y_0$

a tím dostaneme

$\frac{(y_0)^{3/2}}{\sqrt{\alpha}}\int_{1}^{y_1/y_0} \frac{1}{\sqrt{\frac{1}{q } - 1}} {\rm d} q =- t$

pozn.: Vždy je dobré pro lepší průnik do problému, separovat fundamentální konstanty mimo integrál a když nám k tomu pomůže šikovná substituce, zjednoduší se problém. Tohle je bohužel dodnes jedna z úprav, která pro počítací stroje se symbolickými úpravami ještě stále zaostává. Nicméne v tomto tvaru dopočítáme intgrál najítím primitivní funkce (na to nám postačí už starý dobrý wolfram)

$\sqrt{y_0 y_1 (y_0-y_1)} + \sqrt{y_0^3} {\rm ArcCos} \left(\sqrt{y_1/y_0}\right) = t \sqrt{\alpha}$

y0 máme pčáteční vzdálenost a y1 je výsledná. Vidímme, že parametr \alpha hraje roli "škálování času". Stačí si tedy vyřešit problém pro nějaké \alpha a pro jinou hodnotu bude situace obdobná.

Najít konečné řešení y_1 již vyžaduje hledání inverze, která je sice komplikovaná, nicméně výpočetní metoda jistě bude obsahovat superkonvegenci (chyba výsledku bude exponenciálně klesat k počtu iterací metody - což již nemá dál smysl odlišovat od explicitních vyjádření elementárních funkcí, které se v superkonvergenci počítají taky, včetně takové odmocniny).

PS: Komentar k onomu "minus u t", který jsem slibil, ale nechal si ho nakonec. Vyse uvedena rovnice je kadraticcka v deerivaci y podle t. Uprava rovnice tedy muze jit dvěma zpusoby. Tu musíme byt opatrni. Rovnice nam ve fyzikalni interpretaci porovnava kinetickou a potencialni enrgii. Pro zachovani energie muzeme v kazdem kroku ostre zmenit orientaci rychlosti (jakobychom se odrazili od steny) a zákon zachovani energie neutrpi na platnosti. Presto se ale bude jednat o nefyzikalni reseni, protoze zadne odrazy nepředpokládáme. Je pro to potreba volit znemanko z trochu fyziklni pohledu, aby to odpovídalo situaci - totiz ze body se v prubehu casu k sobe priblizuji.

rughar · 18. 06. 2015 17:25

A tady je graf. Můžeme celkem jasně nakreslit graf závislosti dráhy a času (škálujeme celkovým časem, jak dlouho trvá dopad a počáteční vzdáleností).

rss · 19. 06. 2015 09:41 — Editoval rss (19. 06. 2015 09:44)

pietro napsal(a):
↑ rss: Aspoň akási grafická predstava , odhad, ako by mala vyzerať trajektória

v polohočase.

Autor skryl část textu. Zobrazit/skrýt!
Skrytý text:
http://forum.matweb.cz/upload3/img/ … rajekt.PNG

Ďakujem, viem si predstaviť graf pre vzdielnosť-čas. Ale potrebujem vzorec na výpočet vzdialenosti pre počítačovú simuláciu. Potrebujem aby bol vzorec optimalizovaný na presnosť niekoľko platných čísel. Tvoju simuláciu v Calci som nepochopil.

PS: Ak niekto tvrdí že ide o ľahký výpočet, prečo ho ešte neurobil?

rughar · 19. 06. 2015 13:02 — Editoval rughar (19. 06. 2015 17:54)

↑ rss:

Já si například myslím, že výpočet vskutku jednoduchý je. A výsledek jsem dopracoval sem

$\sqrt{y_0 y_1 (y_0-y_1)} + \sqrt{y_0^3} {\rm ArcCos} \left(\sqrt{y_1/y_0}\right) = t \sqrt{\alpha}$

Asi to moc nikdo nedělal ani ne tak pro to, jestli je to lehké/složité, ale že to nejspíš není tolik zajímavé. Minimálně se to moc nepozoruje. Ve vesmíru se spíš objekty nepohybují ostře směrem k sobě. Tohle je zkrátka hodně specifická úloha.

Pro simulaci je hodně důležité, co se po nás chce. Může se chtít:

1) Znát polohu v konkrétním čase
2) Znát celý časový průběh

Pro první bod není potřeba znát celý časový průběh. Pro druhý bod, když už známe řešení pro prvních několik časů, můžeme tuto informaci využít na výpočet v jiném čase. Osobně si myslím, že ale stejně nejrychlejší metoda stále vede přes rovnici, kterou jsem tu výše napsal.

Převedeme to do značení, které je uvedeno v úvodu. Snažíme se počítat dráhy "S" a "s". Výpočet tedy pak může proběhnout po dalších úpravách a zjednodušeních takto

S = R*z
s = r*z

přičemž z je neznámá, kterou získáme jako řešení rovnice

$\sqrt{z (1-z)} + {\rm ArcCos} \left(\sqrt{z}\right) = t \sqrt{\frac{2G(m+M)}{(r+R)^3}}$

Na pravé straně je čas t a pak pod odmocninou všechny fyzikální konstanty a hodnoty počátečních podmínek.

Pukud tedy známe polohu, tak z ní velmi jednoduše zrekonstrujeme přesný čas. Metodou půlení intervalů tak můžeme řešit obrácenou úlohu, kde hledáme polohu, známe-li čas. Je dobré mít na paměti, že čas t může nabývat maximální hodnoty

$\frac{\pi}{2}\sqrt{\frac{(r+R)^3}{2G(m+M)}} = t_{\rm max}$

To je přesně chvíle, kdy body do sebe narazí.

---------------

Po editaci přidávám ještě jednu možnou formulaci. Problém lze i přparametrizovat a napsat rovnice ve tvaru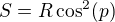

$S=R \cos^2 (p)$ ,
$s=r \cos^2 (p)$ ,

kde 'p' získáme z

$p + \sin(p)\cos(p) = t \sqrt{\frac{2G(m+M)}{(r+R)^3}}$

nebo z totožného vyjádření

$p + \frac{\sin(2p)}{2} = t \sqrt{\frac{2G(m+M)}{(r+R)^3}}$

pietro · 22. 06. 2015 11:34

↑ rughar:Ahoj, vďaka za Tvoj príspevok spojitého riešenia problému.

Zaujímam sa v ďaľšom ešte o rýchlosť približujúcich sa hmotných bodov.

Keď sa dostanú na vzdialenosť veľmi blízku = zrovnateľnú so Schwarzschildovými polomermi,

čo nám z toho vyplynie.

rughar · 23. 06. 2015 17:49

↑ pietro:

No tak na takové blízkosti, pokud chceme počítat se Schwarzschildovým poloměrem, tak už minimálně celý popis bude vypadat trochu jinak. Už si musíme vyjádřit i samotnou rychlost jiným způsobem (protože existuje vícero pozorovatelů s odlišným způsobem měře í rychlosti, tak si musíme některou z nich volit).

V klasickém případě rychlost diverguje. To ale není až tolik podezřelé. Znamená to jen, že okamžitá rychlost nemá smysl. Ale průměrná rychlost na libovolném nenulovém konečném časovém intervalu bude konečná.

$\frac{1}{2}\left(\frac{\mathrm{d}y}{\mathrm{d}t }\right)^2 = \frac{G(m_1+m_2)}{y} - \frac{G(m_1+m_2)}{y_0}$

Odtud se dá získat klasická okamžitá rychlost přímo jako funkce vzdálenosti (je to vlastně součet rychlostí, ale dílčí rychlosti pak lze dopočítat, protože splňují zachování celkové hybnosti).

V relativistickém případě to bude znatelně jinak. Pokud se objekty dostanou na hranu Schwarzschildovým poloměrům, tak se do sebe navzájem pohltí a zůstanou na místě. Velká část energie se uvolní v podobě gravitačních vln.

Co je spíš zajímavé, že pravděpodobně z pohledu jedné padající částice se setkají a pohltí, ale z vnějšího pohledu vněšího pozorovatele se k sobě nejspíš nikdy v konečném čase dočista nepřiblíží.

rss · 23. 06. 2015 20:07 — Editoval rss (23. 06. 2015 20:09)

Vyjadril som X = okamžitú vzdialenosť http://s9.postimg.org/aw77s8wp9/kubikgravitacia.png . Potrebujem vyjadriť jedno reálne X, a optimalizovať zápis pre výpočet pročítačom - jednoduchý zápis a presný výpočet, Opn Office Calc záporné odmocniny nepočíta.

Brzls · 23. 06. 2015 22:05

↑ rss:
Škoda, že to je špatně...

rss · 24. 06. 2015 14:10

Brzls napsal(a):
↑ rss:
Škoda...

Škoda že blafuješ.

Brzls · 25. 06. 2015 00:38

↑ rss:
Používáš vztahy pro rovnoměrně zrychlený pohyb. s=0.5at*t neplatí jen tak univerzálně, to prostě platí jen pro pohyb s konstantním zrychlením (a s počáteční nulovou rychlostí). Jenže tady se zrychlení mění s polohou, tedy tvoje rovnice neplatí, a celý postup i s výsledkem je prostě mimo. Je potřeba vyjít z newtonova zákona, výsledek už tu ukázal rughar. Pokud to hodláš ignorovat, jak je libo...

rss · 26. 06. 2015 07:54 — Editoval rss (26. 06. 2015 08:08)

rughar napsal(a):
↑ rss:Já si například myslím, že výpočet vskutku jednoduchý je. [...]

Ak je to jednoduché, skús vyjadriť okamžitú vzdialenosť (r) ako funkciu času (t), počiatočnej vzdialenosti (R), gravitačnej konštanty (k), hmotností telies (m, M), počiatočná rýchlosť je nulová.

Brzls · 26. 06. 2015 11:02

Inu pokud si to nedokážeš přečíst a přeznačit sám, tak tedy

$\sqrt{R r (R-r)} + \sqrt{R^3} {\rm ArcCos} \left(\sqrt{r/R}\right) = t \sqrt{2k(M+m)}$
problém vyjádřit r explicitně tu již byl také zmíněn. Funkce ArcCos je funkce inverzní k funkci cosinus.

rss · 26. 06. 2015 11:11 — Editoval rss (26. 06. 2015 13:52)

Brzls napsal(a):
Inu pokud si to nedokážeš přečíst a přeznačit sám, tak tedy

$\sqrt{R r (R-r)} + \sqrt{R^3} {\rm ArcCos} \left(\sqrt{r/R}\right) = t \sqrt{2k(M+m)}$
problém vyjádřit r explicitně tu již byl také zmíněn. Funkce ArcCos je funkce inverzní k funkci cosinus.

Prečo to "r" nevyjadríš ty, keď je to také jednoduché?

pietro · 26. 06. 2015 15:29

↑ rss: Ahoj, dobre si to definoval. tam je ten celý zádrhel.

r nejde vyjadriť doteraz používanými metódami symbolicky. ( snáď v budúcnosti to niekto urobí).

Ale kolega rughar nám zabezpečil aspoň, že si môžeme vypočítať t, na základe vstupných rôznych hodnôt r.

čiže poskytol nám inverznú t=t(r).

Ani stroje nepomohli :-(

http://www.wolframalpha.com/input/?i=in … %29%29%3Dy

(no result found in terms of standard mathematical functions)

ani tento

https://www.symbolab.com/solver/functio … gin=button

ani tento

http://www.numberempire.com/inversefunc … ulator.php

ale aspoň si pozrieme bohaté reklamy na kadečo nepodstatné....

====================================================================

Ako sa teda postaviť ku takejto simulácii, keď poznáme inverz...neviem teraz sa vyjadriť.

pietro · 26. 06. 2015 19:09

Alebo, keď poznáme derivácie inverznej funkcie podľa tohoto Odkazu

snáď by sa dal použiť Taylorov rozvoj ....

Matematické Fórum

#1 15. 06. 2015 12:04 — Editoval rss (16. 06. 2015 07:51)

okamžitá vzdialenosť gravitačného priťahovania

#2 15. 06. 2015 12:09 — Editoval rss (16. 06. 2015 09:03)

Re: okamžitá vzdialenosť gravitačného priťahovania

#3 15. 06. 2015 17:24 — Editoval pietro (15. 06. 2015 17:26)

Re: okamžitá vzdialenosť gravitačného priťahovania

#4 15. 06. 2015 17:39 — Editoval rughar (15. 06. 2015 17:40)

Re: okamžitá vzdialenosť gravitačného priťahovania

#5 16. 06. 2015 07:55 — Editoval rss (16. 06. 2015 08:00)

Re: okamžitá vzdialenosť gravitačného priťahovania

rughar napsal(a):

rughar napsal(a):

#6 16. 06. 2015 09:06 — Editoval rss (16. 06. 2015 10:02)

Re: okamžitá vzdialenosť gravitačného priťahovania

pietro napsal(a):

pietro napsal(a):

#7 16. 06. 2015 21:32

Re: okamžitá vzdialenosť gravitačného priťahovania

#8 16. 06. 2015 23:01

Re: okamžitá vzdialenosť gravitačného priťahovania

#9 17. 06. 2015 14:56

Re: okamžitá vzdialenosť gravitačného priťahovania

#10 18. 06. 2015 17:01

Re: okamžitá vzdialenosť gravitačného priťahovania

#11 18. 06. 2015 17:25

Re: okamžitá vzdialenosť gravitačného priťahovania

#12 19. 06. 2015 09:41 — Editoval rss (19. 06. 2015 09:44)

Re: okamžitá vzdialenosť gravitačného priťahovania

pietro napsal(a):

#13 19. 06. 2015 13:02 — Editoval rughar (19. 06. 2015 17:54)

Re: okamžitá vzdialenosť gravitačného priťahovania

#14 19. 06. 2015 13:04 Příspěvek uživatele Brzls byl skryt uživatelem Brzls. Důvod: pozdě

#15 22. 06. 2015 11:34

Re: okamžitá vzdialenosť gravitačného priťahovania

#16 23. 06. 2015 17:49

Re: okamžitá vzdialenosť gravitačného priťahovania

#17 23. 06. 2015 20:07 — Editoval rss (23. 06. 2015 20:09)

Re: okamžitá vzdialenosť gravitačného priťahovania

#18 23. 06. 2015 22:05

Re: okamžitá vzdialenosť gravitačného priťahovania

#19 24. 06. 2015 14:10

Re: okamžitá vzdialenosť gravitačného priťahovania

Brzls napsal(a):

#20 25. 06. 2015 00:38

Re: okamžitá vzdialenosť gravitačného priťahovania

#21 26. 06. 2015 07:54 — Editoval rss (26. 06. 2015 08:08)

Re: okamžitá vzdialenosť gravitačného priťahovania

rughar napsal(a):

#22 26. 06. 2015 11:02

Re: okamžitá vzdialenosť gravitačného priťahovania

#23 26. 06. 2015 11:11 — Editoval rss (26. 06. 2015 13:52)

Re: okamžitá vzdialenosť gravitačného priťahovania

Brzls napsal(a):

#24 26. 06. 2015 15:29

Re: okamžitá vzdialenosť gravitačného priťahovania

#25 26. 06. 2015 19:09

Re: okamžitá vzdialenosť gravitačného priťahovania

Zápatí