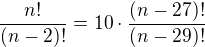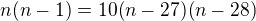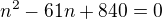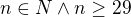Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 25. 06. 2015 14:22

Panassino
Příspěvky: 224
Pozice: student
Reputace:   12 
 

Varice

Zdravím,

Zadání:

Zmenší-li se počet prvků o 27, zmenší se počet variací druhé třídy bez opakování vytvořených z těchto prvků desetkrát. Určete původní počet prvků.

Můj postup: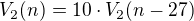$V_{2}(n)=10 \cdot V_{2}(n-27)$

Výsledek by měl být n=40.

Najde se někdo ochotný, kdo mi prozradil co dělám špatně? Děkuji

Offline

  • (téma jako vyřešené označil(a) Panassino)

#2 25. 06. 2015 15:01

gadgetka
Příspěvky: 8562
Škola: Gymnázium Nové Město na Moravě (1985)
Pozice: maminka
Reputace:   462 
 

Re: Varice

Ahoj, asi jen v úpravě a výpočtu. Zápis máš dobře.

Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...

Offline

 

#3 25. 06. 2015 15:03

gadgetka
Příspěvky: 8562
Škola: Gymnázium Nové Město na Moravě (1985)
Pozice: maminka
Reputace:   462 
 

Re: Varice

$\frac{n!}{(n-2)!}=10\cdot \frac{(n-27)!}{(n-29)!}$
$n(n-1)=10(n-27)(n-28)$

Po úpravě řešíš kvadratickou rovnici:
$n^2-61n+840=0$

Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...

Offline

 

#4 25. 06. 2015 17:45 — Editoval Al1 (26. 06. 2015 10:34)

Al1
Příspěvky: 7782
Reputace:   540 
 

Re: Varice

Zdravím,

a podmínky jsou takové, že $n\in N\wedge n\ge 29$

Offline

 

#5 25. 06. 2015 23:04

Panassino
Příspěvky: 224
Pozice: student
Reputace:   12 
 

Re: Varice

↑ gadgetka:

Děkuji, byla chyba ve výpočtu..
Zajímavý je, že asi 5x po sobě jsem tvrdil, že 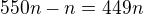$550n-n=449n$..
Proto mi to nevycházelo :D

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson