Matematické Fórum

Rumburak

Ahoj.

Abych se v těchto vedrech poněkud odreagoval od běžných záležitostí, pohrával jsem si trochu se středoškolskou geometrií
a při tom jsem došel ke vztahu, který jsem doposud neznal. Vzhledem k tomu, že mi připadá docela zajímavý, rozhodl jsem se
ho zde uvést. Pokud tak již učinil někdo přede mnou, což je při tom množství příspěvků i přispívajících docela pravděpodobné,
tak se omlouvám.

Nechť 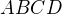$ABCD$ je tětivový čtyřúhelník (takový, jemuž lze opsat kružnici). Označme $M$ průsečík jeho úhlopříček $AC, BD$ .
Potom ptatí

$\frac{|AB|^2}{|MA|\cdot |MB|} = \frac{|CD|^2}{|MC|\cdot |MD|}$ .

Dokažte.

(Symbol 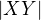$|XY|$ značí délku úsečky $XY$ .)