Matematické Fórum

Pritt · 09. 10. 2015 00:13

Zdravím, chtěl bych se zeptat na správnost mého postupu. Chci ukázat, že množina racionálních čísel $\mathbb{Q}$ je číselné těleso.
Nechť $\mathbb{Q}=\{ \frac{m}{n} |m,n\in \mathbb{Z}\}$
Aby $\mathbb{Q}$ bylo číselné těleso musí splňovat následující:
$(\forall m,n,k,l \in \mathbb{Z}) (\frac{m}{n},\frac{k}{l} \in \mathbb{Q}) \nl 1)(n<>0,l<>0) \frac{m}{n}+\frac{k}{l} \in \mathbb{Q} \nl 2) (n<>0,l<>0) \frac{m}{n}*\frac{k}{l}\in\mathbb{Q} \nl 3)-\frac{m}{n} \in \mathbb{Q} \nl 4) (n<>0,m<>0)(\frac{m}{n})^{-1} \in \mathbb{Q}$
A musí mít alespoň dva prvky.

Teď pokud bych chtěl ukázat, že splňuje 1): $\frac{m}{n}+\frac{k}{l}=\frac{m*l+n*k}{n*l}$
Takže opět dostanu nějaké celé číslo jak ve jmenovateli tak v čitateli, takže součet dvou čísel musí ležet v Q.
2) $\frac{m}{n}*\frac{k}{l}=\frac{m*k}{n*l}$
Vynásobením dvou celých čísel opět dostanu číslo celé, takže toto musí také ležet v Q.
3) $-(\frac{m}{n})=\frac{(-1)*m}{n}=\frac{m}{(-1)*n}$
Což je zase násobení dvou celých čísel, takže opačný prvek taky leží v Q.
4) $\frac{n}{m}$ jako podíl dvou celých čísel musí být tedy prvkem Q.

Protože je pro mě tohle uplně něco nového, byl bych rád, kdybych věděl, co je správné.
Díky za reakce.

Rumburak

↑ Pritt:

Ahoj.

Zde jde o dvě věci:

1) jakým způsobem je množina $\mathbb{Q}$ všech rac. čísel sestrojena z čísel celých ,

2) jakým způsobem jsou definovány algebraické operace (v prvé řadě součet a součin,
ve druhé řadě rozdíl a podíl) s racionálními čísly.

Ad 1.

Mějme množinu 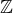$\mathbb{Z}$ všech celých čísel při obvyklém uspořádání a s obvyklými operacemi
součtu a součinu. Příjměme stanovisko, že rac. čísla ještě neznáme.

Idea: Za racionální číslo lze považovat usp. dvojici $[p, q] \in \mathbb{Z}\times (\mathbb{Z} - \{0\})$
(později ukážeme, že $[p, q] = \frac{p}{q}$ , avšak prozatím by zápis vpravo nebyl korektní, protože
dělit celé číslo celým číslem doposud umíme jen tehdy, když tato operace vede k celočíselnému
výsledku). Při tom chceme, aby pro dvě celá čísla $[p, q] , [m, n]$ platila formule

$([p, q] = [m, n]) \Leftrightarrow (pn = qm)$

(odpovídající formuli $$\frac{p}{q} = \frac{m}{n}$ \Leftrightarrow (pn = qm)$ , jejíž naplnění chceme zaručit,
až oba zlomky budou mít smysl).

Technické provedení: Položme $W := \mathbb{Z}\times (\mathbb{Z} - \{0\})$ a na $W$ definujme relaci $\sim$ předpisem

$([p, q] \sim [m, n]) \Leftrightarrow (pn = qm)$ .

Není těžké ukázat, že jde o ekvivalenci na množině $W$ . Tato ekvivalence nám rozdělí množinu $W$
na navzájem disjunktní rozkladové třídy. Označme $[p, q]^*$ právě tu rozkladovou třídu, která obsahuje
usp. dvojici $[p,q] \in W$ (říkáme pak, že $[p, q]$ je representantem třídy $[p, q]^*$ ) , neboli

(*) $[p, q]^* := \{[m,n] \in W ; [p, q] \sim [m, n] \}$ ,

což lze považovat za provisorní zápis zlomku $\frac{p}{q}$ , dokud ještě není zavedeno dělení v plné šíři.
Zřejmě platí

$([p, q]^* = [m, n]^*) \Leftrightarrow ([p, q] \sim [m, n])$ .

Nyní položme

$\mathbb{Q} :=\{ [p, q]^* ; [p, q] \in W \}$

a tuto množinu nazvěme množinou všech racionálních čísel. Celá čísla můžeme vnořit do čísel racionálních
tak, že celému číslu $p$ přiřadíme rac. číslo $[p, 1]^*$ , speciálně celému číslu $0$ odpovídá rac. číslo $[0, 1]^*$ .

Ad 2.

Na výše definované množině $\mathbb{Q}$ zavedeme nejprve algebraické operace:

$[p, q]^* + [r, s]^* := [ps + qr, qs]^*$ ,

$[p, q]^* \cdot [r, s]^* := [pr, qs]^*$ .

Předně nutno dokázat, že tyto definice nejsou závislé na volbě representantů rozkladových tříd.
V dalších krocích lze v oboru $\mathbb{Q}$ dokázat platnost známých aritmetických zákonů
a vět o řešitelnosti rovnic

$a + x = b , cx = d (c \ne 0)$ ,

což dává v oboru rac. čísel operaci rozdílu a operaci podílu.

Uspořádání rac.č. pak můžeme zavést formulemi

$([p, q]^* > [0, 1]^*) \Leftrightarrow ((p > 0 \wedge q > 0) \vee (p < 0 \wedge q < 0))$ ,

$([p, q]^* > [m, n]^*) \Leftrightarrow ([p, q]^* - [m, n]^* > [0, 1]^*)$ .

Je potřeba dokázat, že jde o uspořádání (a před tím ještě nezávislost předchozích formulí na volbě
represntantů tříd) a také vlastnosti tohoto uspořádání ve vztahu k aritmetickým operacím.

vanok · 10. 10. 2015 19:37

Pozdravujem,
Tu najdes https://en.m.wikipedia.org/wiki/Rational_number
popis konstrukcie struktury Q.
Uvidis, ze ta je urobena tak aby (Q, +,.) bolo komutativne teleso (= pole).

Pritt · 11. 10. 2015 10:44

Děkuji vám oběma.

Matematické Fórum

#1 09. 10. 2015 00:13

Důkaz: Q je číselné těleso

#2 09. 10. 2015 16:12 — Editoval Rumburak (10. 10. 2015 12:21)

Re: Důkaz: Q je číselné těleso

#3 10. 10. 2015 19:37

Re: Důkaz: Q je číselné těleso

#4 11. 10. 2015 10:44

Re: Důkaz: Q je číselné těleso

Zápatí