Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Porovnání kombinačních čísel (TOTO TÉMA JE VYŘEŠENÉ)
#1 11. 10. 2015 16:33
Porovnání kombinačních čísel
Zdravím,
upravte a porovnejte: (6n nad 3) a (3n nad 6).
Potreboval bych poradit s temi upravami.
Kdyz si to rozepisu tak mi vznikne dlouhy vyraz a nevim co s nim dal ?

Mel bych urcit pro ktere n je vetsi prvni vyraz a pro ktere druhy..
Offline
- (téma jako vyřešené označil(a) kucape)
#3 11. 10. 2015 17:31 — Editoval kucape (11. 10. 2015 17:32)
Re: Porovnání kombinačních čísel
↑ zdenek1:
Co presne mam roznasobit?
Protoze kdyz roznasobim  tak mi vyjde
tak mi vyjde  ..
..
Offline
#5 12. 10. 2015 17:26 — Editoval kucape (12. 10. 2015 17:28)
Re: Porovnání kombinačních čísel
↑ OndrasV:
Ano samozejme, myslel jsem, ze mi vyjde obecne polynom ctvrteho radu.
Kdyz to roznasobim tak mi vyjde: 
tedy 
Ale porad mi unika jak z toho dostat reseni.
Offline
#6 12. 10. 2015 18:54 — Editoval Brano (12. 10. 2015 19:30)
Re: Porovnání kombinačních čísel
principialne sa daju kvarticke rovnice riesit vzorcom - ktory je dost hnusny, ale teba aj tak zaujmaju iba celociselne riesenia, takze si to uprav do zakladneho tvaru
t.j. po prehodeni a skrateni  mas
mas
(prosim over si to kvoli preklepom)
no a celociselne korene takejto rovnice musia byt nutne delitele posledneho clena - t.j. delitele 200
- to je konecne vela moznosti na overenie tak vela trpezlivosti :D
ale da sa skusat aj tak rozumne - samozrejme tie "tipy" sa budu lepsie dosadzat do tohoto
a da sa urobit aj odhad na velkost  - mozes si tu rovnicu upravir takto
- mozes si tu rovnicu upravir takto
lava strana je priblizne  a prava strana je priblizne
a prava strana je priblizne  co ti da
co ti da 
tak najprv vyskusaj delitele 200 okolo tohoto cisla - konkretne  a
a 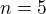
tie nevyjdu (dalsie njblizsie su 2 a 8 - tiez nic) tak uz hned mozes tusit, ze asi to celociselne riesenie nebude mat, len bez nejakych presnejsich odhadov budes musiet aj tak vyskusat vsetky a nakoniec ti vyjde, ze to ziadne celociselne riesenie nema
Offline
#8 12. 10. 2015 20:45
Re: Porovnání kombinačních čísel
↑ kucape:
jaj, no tak to treba polozit otazku spravne - ty si sa tam pytal na rovnost a ta nenastava (pre cele cisla)
v tom pripade sa ti hodia vsetky realne korene - jeden je prave okolo tych  a preto je prave tam deliaci bod - t.j. 2,3,4 a potom 5,...
a preto je prave tam deliaci bod - t.j. 2,3,4 a potom 5,...
riesenie skusim najst nejake jednoduche
Offline
#10 12. 10. 2015 21:41
Re: Porovnání kombinačních čísel
↑ kucape:
ved hej - ja som to neporiadne precital
takze asi taky najpriamociarejsi postup co ma napadol je takyto:
chceme zistit znamienko funkcie pre
pre  to proste dosad a dostanes ze je to zaporne
to proste dosad a dostanes ze je to zaporne
pre 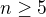 budeme chciet dokazat, ze je to kladne - substituujme
budeme chciet dokazat, ze je to kladne - substituujme  a teda mame
a teda mame 
a skumame
vypocitajme a teda pre
a teda pre  mame
mame
a to spolu s tym, ze  nam indukciou zaruci, ze pre
nam indukciou zaruci, ze pre  plati
plati  a teda pre
a teda pre 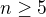 plati
plati 
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Porovnání kombinačních čísel (TOTO TÉMA JE VYŘEŠENÉ)


 .
. je vetsi (6n nad 3) a pro
je vetsi (6n nad 3) a pro  je vetsi (3n nad 6).
je vetsi (3n nad 6).