Matematické Fórum

Freedy · 12. 10. 2015 20:18

Dobrý den,

tak je zkrátka možné, že věci vůbec nechápu, to nemůžu vyloučit.
Nicméně, nedostatečné vysvětlení (i po otázání) mě vede k tomu, zeptat se tady.

Pokud mám uspořádanou dvojici 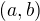$(a,b)$ tak tato tvrzení jsou nepravdivá:
$a\in (a,b)$
$b\in (a,b)$
správně?

Protože jelikož se uspořádaná dvojice definuje následovně:
$(a,b)=\{\{a\},\{a,b\}\}$ tak potom tedy tato tvrzení jsou pravdivá:
$\{a\}\in (a,b)$
$\{a,b\}\in (a,b)$

chápu to správně?

Freedy

Brano · 12. 10. 2015 20:23 — Editoval Brano (12. 10. 2015 20:29)

v tomto pripade ano, aj ked toto
$(a,b)=\{\{a\},\{a,b\}\}$
nie je kanonicke - su aj ine moznosti definovania usporiadanej dvojice, ale tym sa nemusis trapit pracuj s tou jednou definiciou ktora sa pouziva v knihe co citas

len pre zaujimavost
https://en.wikipedia.org/wiki/Ordered_pair

Ta co pouzivas je Kuratowskeho - a mne sa zda najelegantnejsia

Freedy · 12. 10. 2015 20:45

↑ Brano: Ahoj

koukal jsem na článek a je u té Kuratowské metody napsané toto:
Pokud jsou ty složky stejné, potom platí:
$(x,x)=\{\{x\},\{x,x\}\}$ --- tohle ještě chápu. To je stejný princip jako ^
Nicméně proč se pak pokračuje v rovnítkách a pokračuje to:
$\{\{x\},\{x,x\}\}=\{\{x\},\{x\}\}$
vždyť přece $\{\{x\},\{x\}\}$ tato neuspořádaná množina má pouze jeden prvek. Tedy je to množina $\{\{x\}\}$
To však není to samé jako uspořádaná dvojice (x,x) ne?

Díky za reakci

byk7 · 12. 10. 2015 21:01

↑ Freedy:

Právě že z definice plyne, že $(x,x)=\{\{x\}\}$ . :-)

Ono to má i svou logiku, ty chceš v množině 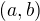$(a,b)$ rozlišit, který prvek je první a to uděláš právě tím způsobem $\{\{a\},\{a,b\}\}$ . Pokud jsou ale dva prvky stejné, tak je jedno, který z těch dvou stejných prvků bude první, ne? :-)

Matematické Fórum

#1 12. 10. 2015 20:18

Prvek množiny - znova

#2 12. 10. 2015 20:23 — Editoval Brano (12. 10. 2015 20:29)

Re: Prvek množiny - znova

#3 12. 10. 2015 20:45

Re: Prvek množiny - znova

#4 12. 10. 2015 21:01

Re: Prvek množiny - znova

Zápatí