Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Důkaz věty nejkratší vzdálenosti dvou bodů
#1 13. 10. 2015 20:29
Důkaz věty nejkratší vzdálenosti dvou bodů
Zdravím vás!
Lámu si hlavu nad tím, jestli se dá dokázat věta níže napsaná. Prosím pomozte mi důkaz kriticky ohodnotit, co v něm chybí, co je špatně, a tak.
Věta: Nechť jsou v rovině (pohybuji se jen v rovině) dány dva různé body  ,
,  . Pak nejkratší vzdálenost od
. Pak nejkratší vzdálenost od  do
do  je délka úsečky
je délka úsečky  .
.
Důkaz: Úsečka  s krajními body
s krajními body  ,
,  je jediná rovná křivka, jenž body spojuje. Jakoukoli nerovnou křivku
je jediná rovná křivka, jenž body spojuje. Jakoukoli nerovnou křivku  vedenou z
vedenou z  do
do  mohu narovnat na rovnou křivku - úsečku
mohu narovnat na rovnou křivku - úsečku  . Po narovnání do směru
. Po narovnání do směru  již koncový bod pro
již koncový bod pro  nebude totožný s bodem
nebude totožný s bodem  , respektive s bodem
, respektive s bodem  . To znamená, že (
. To znamená, že ( je kratší, než
je kratší, než  )
)  (
( je delší, než
je delší, než  ).
).  je stejně dlouhá jako
je stejně dlouhá jako  , a protože
, a protože  , pak
, pak  . Kdyby
. Kdyby  byla kratší, než
byla kratší, než  , jeden z z bodů
, jeden z z bodů  ,
,  by na
by na  neležel. Proto
neležel. Proto  je delší, než
je delší, než  neboli každá nerovná křivka s koncovými body
neboli každá nerovná křivka s koncovými body  a
a  je delší, než úsečka
je delší, než úsečka  .
. 
Není všechno, co se třpytí, není všechno k pochopení.
Není lehké živobytí, a přesto zloba v nás není.
Offline
#2 13. 10. 2015 20:43
- OndrasV

- Místo: Praha
- Příspěvky: 513
- Škola: VŠE (1997-2004), FEL (2014-??)
- Pozice: mudrlant
- Reputace: 31
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
↑ Makrofág: Zkus použít trojúhelníkou nerovnost, tj. vzdálenost A do B musí být menší nebo rovna vzdálenosti A a C a vzdálenosti C a B.
Offline
#3 13. 10. 2015 21:04 — Editoval Makrofág (13. 10. 2015 21:10)
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
↑ OndrasV: Ano, to je pak jednoduché. Zvolím si na křivce  libovolně bod
libovolně bod  , jenž neleží na
, jenž neleží na  a řeknu, že součet vzdálenosti od
a řeknu, že součet vzdálenosti od  do
do  a vzdálenosti
a vzdálenosti  do
do  je větší, než vzdálenost od
je větší, než vzdálenost od  do
do  . Jenže věta, kterou chci dokázat, je vlastně obecný případ trojúhelníkové nerovnosti a na důkaz trojúhelníkové nerovnosti nemůžu používat tuto nerovnost, protože ji dokazuji. To by byl důkaz kruhem. A proto se tě Ondro ptám, jestli je tedy tato věta dokazatelná, nebo není. Já fakt nevím.
. Jenže věta, kterou chci dokázat, je vlastně obecný případ trojúhelníkové nerovnosti a na důkaz trojúhelníkové nerovnosti nemůžu používat tuto nerovnost, protože ji dokazuji. To by byl důkaz kruhem. A proto se tě Ondro ptám, jestli je tedy tato věta dokazatelná, nebo není. Já fakt nevím.
Jinak prosímvás, pokud mi napíšete, že se moje věta bez použití té nerovnosti dokázat nedá, pak chci vědět, v čem můj důkaz není důkazem, v čem prostě kulhá.
Není všechno, co se třpytí, není všechno k pochopení.
Není lehké živobytí, a přesto zloba v nás není.
Offline
#4 13. 10. 2015 21:08 Příspěvek uživatele OndrasV byl skryt uživatelem OndrasV. Důvod: x
#5 13. 10. 2015 21:20
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
Axiomy:
(i) Bod je to, co nemá části
(ii) Úsečka je konečná délka bez šířky
(iii) Přímka je nekonečná délka bez šířky
(iv) Hranicemi úsečky jsou body
(v) Plocha je to, co má délku a šířku
(vi) Hranicemi plochy jsou přímky, nebo úsečky
.
Doplň vše, o čem si myslíš, že je nezbytné pro důkaz. Já si myslím, že tyhle axiomy pro něj stačí. A myslím si, že pokud s těmito axiomy větu nedokážeme, nedokážeme ji ani s více axiomy.
Není všechno, co se třpytí, není všechno k pochopení.
Není lehké živobytí, a přesto zloba v nás není.
Offline
#6 13. 10. 2015 21:37
- OndrasV

- Místo: Praha
- Příspěvky: 513
- Škola: VŠE (1997-2004), FEL (2014-??)
- Pozice: mudrlant
- Reputace: 31
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
↑ Makrofág: Máš nějakou axiomatickou definici trojúhelníka?
Offline
#7 13. 10. 2015 21:48 — Editoval Makrofág (13. 10. 2015 21:50)
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
↑ OndrasV: Mám definici trojúhelníka, ale nevím, co to je axiomatická definice. Beru axiom buďto jako definici vycházející z rozumného popisu, ve kterém axiomy už nejsou, anebo jako nedokazatelný fakt a definici beru jako pro zjednodušení nově vzniklý pojem vzniklý z axiomů. Jak to bereš ty? Třeba mi něco uniká....
Def.: Mějme rovinu E a na ní ležící body  ,
,  a
a  , jenž neleží v přímce. Pak trojúhelník
, jenž neleží v přímce. Pak trojúhelník 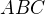 je rovinný útvar vzniklý průnikem:
je rovinný útvar vzniklý průnikem:
a) poloroviny ohraničené přímkou  , kde v této polorovině leží bod
, kde v této polorovině leží bod 
b) poloroviny ohraničené přímkou 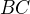 , kde v této polorovině leží bod
, kde v této polorovině leží bod 
c) poloroviny ohraničené přímkou  , kde v této polorovině leží bod
, kde v této polorovině leží bod 
Není všechno, co se třpytí, není všechno k pochopení.
Není lehké živobytí, a přesto zloba v nás není.
Offline
#8 13. 10. 2015 22:04
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
Já ti nevím, ale křivka je dost složitý pojem a operovat něčím jako narovnání mi přijde přinejmenším podezřelé. Jak takové narovnání probíhá? Co znamená "narovnat do směru  "?
"?
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#9 13. 10. 2015 22:17
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
↑ byk7: Já jsem se rozhodl, že na to půjdu jinak. A taky proto, žes mě nachytal a já prostě nevím, jak bych vysvětlil matematicky, co je narovnání křivky. Je to asi dost nejistá cesta teda....
Tak mám ještě otázku byku7, jestli trojúhelníková nerovnost mluví jen o úsečkách vedoucích přes bod  , anebo to mohou být křivky. Chci prostě dokázat, že jakákoliv křivka vedená přes bod
, anebo to mohou být křivky. Chci prostě dokázat, že jakákoliv křivka vedená přes bod  , který tedy na
, který tedy na  neleží, je delší, než
neleží, je delší, než  . Jak bys na to šel? Víc hlav víc ví :-)
. Jak bys na to šel? Víc hlav víc ví :-)
.
Jinak, jak mám zadefinovanou křivku: Křivka je v jedné rovině ležící objekt, u kterého můžeme změřit jen délku.
Není všechno, co se třpytí, není všechno k pochopení.
Není lehké živobytí, a přesto zloba v nás není.
Offline
#10 14. 10. 2015 01:40
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
Radšej to všetko nechaj tak,
"Křivka je v jedné rovině ležící objekt, u kterého můžeme změřit jen délku."
s takouto definíciou nemáš šancu robiť reálne dôkazy.
1^6 - 2^6 + 3^6 = 666
Offline
#11 14. 10. 2015 22:20
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
↑ Makrofág:
Ahoj, obecný důkaz bude asi nutné provést přes variační počet...
"Máte úhel beta." "No to nemám."
Offline
#12 15. 10. 2015 12:51
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
↑ Makrofág: Jukni sem: http://ulozto.cz/xs4pRvug/variacni-ulohy-ve-fyzice-pdf
Je to moje bakalářská práce (v surové podobě). Pokud se prokousáš aspoň do kapitoly 6, tak tam je vidět, že pokud řešení vůbec existuje, pak se musí jednat o úsečku.
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline
#13 23. 10. 2015 14:51
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
Tak se vracím na místo činu, abych téma ukončil, pokud důkaz mé věty před vámi obstojí. Tak zaprvé formálně definuji rovinnou křivku takto:
Def.: Nechť  , dále nechť
, dále nechť  spojité fce
spojité fce  a
a  . Pak rovinná křivka (dále už jen křivka) je rovinný útvar definovaný jako
. Pak rovinná křivka (dále už jen křivka) je rovinný útvar definovaný jako ![kopírovat do textarea $\bigcup_{x\in I}^{}\{[f(x);g(x)]\}$](/mathtex/2c/2c80e1ce4ea7ffda38a9b2967d248a8a.gif) .
.
Zadruhé jsem se smířil s tím, že axiom trojúhelníkové nerovnosti je axiom, budu ho tak brát. Díky Anonymystiku. Mrknu na to. A tak tedy budu dokazovat trochu jinou větu.
Věta: Nechť jsou dány tři různé body  neležící v přímce. Pak křivka
neležící v přímce. Pak křivka  s krajními body
s krajními body  a
a  , vedena bodem
, vedena bodem  , je delší, než
, je delší, než  .
.
Důkaz: Nechť je dána křivka 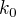 jako sjednocení
jako sjednocení 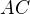 a
a 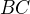 . Pak
. Pak  . Na
. Na 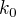 zvolíme různé body
zvolíme různé body  a
a  tak, že
tak, že  , dále zvolíme libovolně bod
, dále zvolíme libovolně bod  . Křivka
. Křivka 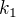 jest definována takto:
jest definována takto:  .
.
a) 
b)  .
.
Při jakémkoli umístění bodu  platí:
platí:  .
.
Stejný postup provedeme na 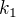 . Najdeme podle stejných kritérií body
. Najdeme podle stejných kritérií body  a
a 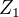 , libovolně zvolíme bod
, libovolně zvolíme bod  , a pak
, a pak  .
.  . Takto můžeme vytvarovat křivku do libovolného tvaru, protože můžeme přidat bodů, kolik chceme. Vždycky totiž najdeme body
. Takto můžeme vytvarovat křivku do libovolného tvaru, protože můžeme přidat bodů, kolik chceme. Vždycky totiž najdeme body  a
a  tak, aby to vyhovovalo našim podmínkám.
tak, aby to vyhovovalo našim podmínkám. .
.
Představme si jakoukoli křivku  s krajními body
s krajními body  ,
,  , která prochází bodem
, která prochází bodem  . Pak tuto křivku podle našeho postupu jsme schopni sestrojit.
. Pak tuto křivku podle našeho postupu jsme schopni sestrojit.
Dík za dočtení. Je tam něco, s čím nesouhlasíte?
Není všechno, co se třpytí, není všechno k pochopení.
Není lehké živobytí, a přesto zloba v nás není.
Offline
#14 27. 10. 2015 01:11
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
↑ Makrofág:
Ahoj, zatím souhlasím se vším. Říkám zatím, protože jsi pouze dokázal větu pro lomennou čáru a nikoli pro obecnou křivku. Asi by to chtělo nějaký lmitní přechod nebo něco podobného. No a nebo ten variační počet.
"Máte úhel beta." "No to nemám."
Offline
#15 29. 10. 2015 15:10
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
Poznamka.
Toto moze pomoct
https://en.m.wikipedia.org/wiki/Geodesic
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 02. 11. 2015 09:53
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
Ozývám se zase po čase....
Zatím s tím nehnu, tak si jdu přečíst tu práci od Anonymystika a článek od Vanoka. Díky. Kdokoliv pište nápady, budu se v tom dále hrabat.
Jinak pro check_drummera: Týká se to jen lomených čar proto, že tím postupem vytvořím konečné množství bodů, a to znamená, že body na té křivce budou spojeny vždycky úsečkami? Ptám se na to, jestli bez použití limit můžu stvořit křivku, která nebude lomenou čarou. Asi ne co?
Není všechno, co se třpytí, není všechno k pochopení.
Není lehké živobytí, a přesto zloba v nás není.
Offline
#17 02. 11. 2015 13:24
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
Makrofág napsal(a):
Ptám se na to, jestli bez použití limit můžu stvořit křivku, která nebude lomenou čarou.
Krivka  pre
pre ![kopírovat do textarea $t \in [0,1]$](/mathtex/1d/1df957bdb2587220b720234dddf2c28f.gif) je stvrtkruznica. Nie je to lomena ciara a predsa sa v definicii nevyskytuje limita. Je to proste parametrizovana mnozina bodov.
je stvrtkruznica. Nie je to lomena ciara a predsa sa v definicii nevyskytuje limita. Je to proste parametrizovana mnozina bodov.
Tvoj problem je ten, ze predpokladas, ze "krivka" je to co si predstavujes. Matematika sice je obmedzena ludskou predstavivostou, ale nie takto.
Offline
#18 03. 11. 2015 00:45
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
Ahoj,
napadá mě, že pokud by bylo možné zkoumanou křivku transformovat na funkci f, tak by bylo možné využít vztah pro délku křivky " ". A pokud f není konstantou (úsečkou rovnoběžnou s osou x), tak je
". A pokud f není konstantou (úsečkou rovnoběžnou s osou x), tak je  pro nějaké t (a tedy i na nějakém okolí bodu t) - a tedy délka f bude delší než délka oné úsečky - pro kterou je vždy f'=0.
pro nějaké t (a tedy i na nějakém okolí bodu t) - a tedy délka f bude delší než délka oné úsečky - pro kterou je vždy f'=0.
Nejsem si ale jist, zda se někde při odvození toho vzorce nepředpokládá, že úsečka je nejkratší spojnice dvou bodů...
"Máte úhel beta." "No to nemám."
Offline
#19 03. 11. 2015 00:51
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
↑ check_drummer:
Ak si dobre pametam, slo o Riemannov integral ako limitny prechod od nasekania na usecky. Hups. Postulovat by to samozrejme slo, kazdopadne potom by tam bola asi kopa inych veci na dokazanie.
Offline
#20 03. 11. 2015 01:03
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
↑ Xellos:
Pak si ovšem položme otázku, co je to délka křivky?... :-)
"Máte úhel beta." "No to nemám."
Offline
#21 04. 11. 2015 09:33
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
↑ check_drummer:
V tomto pripade samozrejme limita dlzky vypocitanej ako sucet dlzok useciek (ak max. dlzka usecky ide k nule).
Offline
#22 05. 11. 2015 00:50
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
↑ Xellos:
A proč jako součet délky úseček - odkud víme, že úsečka je nejkratší spojnice? :-) A jsme, zdá se v kruhu...
"Máte úhel beta." "No to nemám."
Offline
#23 06. 11. 2015 15:23
- Eratosthenes
- Příspěvky: 2592
- Reputace: 132
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
ahoj ↑ Makrofág:
žonglování "vysokou matematikou" a la ↑ Makrofág: tvému "důkazu" vážnosti nedodá. Zvlášť když v něm používáš takové pojmy jako "narovnání křivky", "vytvarování křivky" apod. S trojúhelníkovou nerovností jako axiomem se smiřovat nemusíš. Ta axiomem prostě je - bez ní totiž pojem "vzdálenost" vůbec nemá smysl (vygogluj si něco o metrickém prostoru). No a pak na té větě není prakticky co dokazovat, protože plyne bezprostředně z tohoto axiomu.
Budoucnost patří aluminiu.
Offline
#24 07. 11. 2015 19:42
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
Ahoj,
Eratosthenes napsal(a):
... No a pak na té větě není prakticky co dokazovat, protože plyne bezprostředně z tohoto axiomu.
Jak tedy plyne? Resp. jak definuješ délku křivky?
"Máte úhel beta." "No to nemám."
Offline
#25 07. 11. 2015 19:58 — Editoval Eratosthenes (07. 11. 2015 20:01)
- Eratosthenes
- Příspěvky: 2592
- Reputace: 132
Re: Důkaz věty nejkratší vzdálenosti dvou bodů
ahoj ↑ check_drummer:
k tomu nepotřebuju definovat křivku, natož její délku. Je to totiž právě naopak. Jestliže neznám délku úsečky, nemůžu definovat délku křivky. Takže:
Axiom: Pro každé tři různé body A,B,C platí:
d(A,B) <= d(AC) +d(CB)
přičemž d(A,B) = d(AC) +d(CB) <=> C in AB.
Tak se definuje vzdálenost v elementární geometrii. Takže tvoje věta vlastně z toho axiomu ani neplyne, ale je přímo axiomem. A axiomy, jak známo, není třeba dokazovat.
Budoucnost patří aluminiu.
Offline
Stránky: 1 2
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Důkaz věty nejkratší vzdálenosti dvou bodů