Matematické Fórum

Zdravím v tématu.

Jako studentovi MFF UK je mi jasné, že není možné, aby matematika byla na všech školách budována stejně precizně jako na matfyzu. Už třeba jen z časových důvodů by to prostě nešlo, a proto jsem ochoten leccos překousnout.

Definice typu "Křivka je v jedné rovině ležící objekt, u kterého můžeme změřit jen délku" je ale na mě příliš.

Děkuji Eratosthenesovi za vnesení matematiky do tématu. Ještě bych rád něco doplnil:

Zvolíme-li na standardní eukleidovskou metriku (budu ji značit 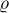), pak je přirozené definovat délku úsečky AB jako a délku lomené čáry jako součet délek dílčích úseček. Eukleidovská metrika splňuje (jako ostatně každá metrika) trojúhelníkovou nerovnost, a tedy je zřejmé, že ze všech lomených čar spojujících dva různé body A, B má nejmenší délku právě úsečka AB.

Pokud jde o pojem křivky, tak ten není v matematice ustálen – v různých oblastech se používají různé definice. Jedna z nejběžnějších je následující:
Křivkou v rozumíme jakoukoli množinu bodů , pro kterou existuje spojité zobrazení (ve smyslu standardní eukleidovské topologie) takové, že .
Poznamenávám, že interval může být v definici ekvivalentně nahrazen intervalem pro jakákoli reálná čísla .

Z této definice hned plyne, že křivka je vždy souvislá kompaktní množina (neboli kontinuum), přičemž kompaktnost je v ekvivalentní se současnou uzavřeností a omezeností (resp. totální omezeností).

V tomto směru tedy tato definice celkem odpovídá naší intuitivní představě křivky. V jiných ohledech se však velmi liší, nicméně to už bych asi odbočoval od tématu.

Délku křivky je přirozené definovat jako supremum množiny délek lomených čar aproximujících danou křivku (jsem líný to psát formálně, tak doufám, že je jasné, co mám na mysli).

Z takovéto definice je hned jasné, že nejkratší křivkou spojující dva různé body v je právě úsečka.

↑↑ Eratosthenes:
Ono by to ani nebylo nutné brát jako axiom, stačí definovat d pomocí analytické geometrie jako (, ) a pak je ovšem snadné ten axiom dokáztat jako větu. Ty jdeš na to opačně a pak asi z těch axiomů vyvodíš zde uvedený tvar d (což ale pro důkaz té věty, kterou tu zkoumáme, není nutné znát).

↑ check_drummer:

>> kdybychom to jako axiom nepřijmuli, tak bychom mohli definovat různé jiné metriky

Kdybychom to jako axiom nepřijali, nebyla by to metrika.

>>To sice je, ale není na první pohled jasné, že je to jediná nejkratší spojnice.

Jak komu:

výrok A: Bod leží na úsečce.
výrok B: Vzdálenost je rovna součtu.

Axiom: A <=> B

Tedy   A' <=> B'

Výrok B':  Vzdálenost není rovna součtu.

A možnost, že je vzdálenost menší, vylučuje trojúhelníková nerovnost.

Co je na tom nejasného

↑ Jenda358:
Myslím, že když se snažíme ukázat, že úsečka je nejkratší spojnicí, tak není vhodné definovat délku křivky pomocí úseček... Jinak na vše ostatní se ta definice hodí výborně.

Eratosthenes napsal(a):

>> kdybychom to jako axiom nepřijmuli, tak bychom mohli definovat různé jiné metriky

Kdybychom to jako axiom nepřijali, nebyla by to metrika.

Šlo mi o to uvažovat takový systém axiomů, který dostatečně "věrně" popisuje Eukleidovský prostor, ale který explicitně (nebo téměř explicitně) netvrdí, že nejkratší spojnicí dvou bodů je úsečka. Ono to ale stejně půjde asi snadno dokázat z jakéhokoli systému axiomů popisující metriku v eukleidovském prostoru. (Viz ta "pythagorejská" metrika.)

↑ Jenda358:
Tady už se spíš než korektním důkazům věnujeme tomu, jak zvolit axiomy a definice, aby vystihovaly naše představy. Zde jsme tedy narazili na to, že intuitivně chápeme úsečku jako nejkratší spojnici dvou bodů - a proto na základě toho definujeme délku křivky jako "limitu" (resp. supremum) délek lomených čar. To je v pořádku - ovšem pokud se začneme ptát, zda je opravdu nejkratší vzdálenost dvou bodů úsečka, tak musíme délku křivky definovat jinak (třeba těmi kruhy) (a nebo to obejít jako Erathostenes a definici křivky nepotřebujeme) - no ale pak lze ukázat, že vlastně obě definice jsou ekvivaletní (možná v nějakých patologických případech nejsou...) a tedy se můžeme pak šťastně vrátit k původní definici s lomennou čarou a zabili jsme tak dvě mouchy jednou ranou.

check_drummer napsal(a):

↑ Jenda358:
pokud se začneme ptát, zda je opravdu nejkratší vzdálenost dvou bodů úsečka

Jádrem našich neshod bude asi odlišné chápání toho, co znamená "opravdu". Možná máš dosti odlišný názor na souvislost matematiky s reálným světem. Já od matematiky apriorně neočekávám, že mi dá odpovědi na otázky týkající se povahy věcí kolem nás (netvrdím, že ty ano, jen vysvětluji svůj přístup). Proto mi také nepřijde nic špatného na tom, když definuji délku křivky tak, jak jsem ji definoval.
Pokud bych ale chtěl důkaz nebo alespoň náznak důkazu toho "opravdu" (v takovém tom hlubším smyslu), pak se rozhodně také nespokojím s definicí délky křivky přes aproximace lomenými čarami.

Abych to shrnul: já zkrátka apriorně nepovažuji za pravdivé či nepravdivé tvrzení, že nejkratší spojnicí dvou bodů v rovině je úsečka. Počkám, až mi někdo dá potřebné definice (nebo si je udělám sám), a pak to buď dokážu, nebo vyvrátím (nebo si nebudu vědět rady :D). Nic víc, nic míň.