Matematické Fórum

herys01 · 18. 10. 2015 21:59

Ahoj,

potřebuji pomoct dopočítat souřadnice dvou bodů (červené křížky) na obrázku.

Znám pouze počáteční a koncové body obou úseček. Nevím jak na to jít. Vím, že body jsou prodloužením úseček (tu polohu nového bodu bych dokázal dopočítat ze směrnice úseček), ale již nedokážu vypočítat délku toho prodloužení "d".. Tuším že to asi někjak půjde přes kolmice oněch úseček, ale nevím bohižel jak.

Díky za radu

//forum.matweb.cz/upload3/img/2015-10/98373_body.png

herys01

↑ Cheop:

To by právě platilo, kdyby ty úsečky byly rovnoběžné s "osou x". Bohužel celý problém je v tom, že úsečky jsou vždy o nějaký úhel orotované, např. mají odchylku s "osou x" 30°. Pak to co jste navrhoval bohužel neplatí. Přidal jsem osy pro názornost:

//forum.matweb.cz/upload3/img/2015-10/36209_body.png

jelena · 19. 10. 2015 11:01

Zdravím,

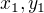můj nástin: obě zadané přímky můžeme popsat rovnici ve tvaru $y=kx+q$ , pro kolmou přímku (např. procházející bodem $x_1, y_1$ na horní přímce) můžeme také odvodit její směrnici $k$ (vztah pro normálu k původní přímce) a také do tvaru $y=kx+q$ . Potom najít průsečík kolmé přímky a spodní přímky (bod "červený křížek" na spodní přímce). Následně najít požadovanou vzdálenost $d$ - viz vzorec pro vzdálenost bodů.

Obdobně, pokud budeme startovat od spodní přímky směrem nahoru. Popsala jsem to srozumitelně a je to použitelné?

Pokud ale problém jen

(tu polohu nového bodu bych dokázal dopočítat ze směrnice úseček), ale již nedokážu vypočítat délku toho prodloužení "d"

tak potom jen vzdálenost bodů v rovině. V tom je problém? Děkuji.

herys01 · 19. 10. 2015 20:26

↑ jelena:

Myslím, že to chápu. Stačí jen určit normálový vektor k přímce, z něho pak vytvořit kolmici v daném bodě a poté najít průsečík.

Díky vyřešeno

jelena · 19. 10. 2015 20:56

↑ herys01: děkuji za zprávu (techniku sestavení rovnice přímky ze 2 bodů a přímky k ní kolmé si určitě můžeš zvolit tak, jak je "technicky pohodlné").

Matematické Fórum

#1 18. 10. 2015 21:59

Výpočet polohy bodů (prodloužení úsečky)

#2 19. 10. 2015 07:58 — Editoval Cheop (19. 10. 2015 07:59) Příspěvek uživatele Cheop byl skryt uživatelem Cheop. Důvod: Špatná úvaha

#3 19. 10. 2015 08:28 — Editoval herys01 (19. 10. 2015 08:30)

Re: Výpočet polohy bodů (prodloužení úsečky)

#4 19. 10. 2015 11:01

Re: Výpočet polohy bodů (prodloužení úsečky)

#5 19. 10. 2015 20:26

Re: Výpočet polohy bodů (prodloužení úsečky)

#6 19. 10. 2015 20:56

Re: Výpočet polohy bodů (prodloužení úsečky)

Zápatí