Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Dokaz iracionality
#1 29. 10. 2015 09:58
Dokaz iracionality
Pozdravujem.
Dalsia diskuzia
Ako by ste dokazali, ze napr. 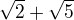 je iracionalne cislo ?
je iracionalne cislo ?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 29. 10. 2015 19:36 — Editoval vanok (29. 10. 2015 19:46)
Re: Dokaz iracionality
Ahoj ↑ Brano:, ↑ Pavel:
Dakujem za prispevky.
To mate pravdu.... Take dokazy sa vidia naajcastejsie.
Ja som myslel na vyuzitie toho, ze ide o algebricke cislo.
Je jednoduche napisat jeho minimalny polynom a lahko sa ukaze ze ten nema rationalny koren.
A tak rozmyslajme este trochu o tom.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 29. 10. 2015 22:53
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: Dokaz iracionality
↑ vanok:
Ahoj,
napadlo mě:
Pokud 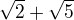 není iracionální, tak lze psát
není iracionální, tak lze psát  a
a  pro i iracionální, r,s racionální (víme, že
pro i iracionální, r,s racionální (víme, že 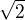 a
a  jsou iracionální). Potom tedy je
jsou iracionální). Potom tedy je  . Ovšem je i
. Ovšem je i 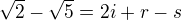 a vynásobením obou rovností získáme 2-5=(r+s).(2i+r-s), z čehož plyne, že i je racionální, což je spor.
a vynásobením obou rovností získáme 2-5=(r+s).(2i+r-s), z čehož plyne, že i je racionální, což je spor.
"Máte úhel beta." "No to nemám."
Offline
#6 29. 10. 2015 23:01
Re: Dokaz iracionality
Ahoj ↑ check_drummer:,
Z trochou prace sa tu podari ukazat pekne metody na ktore ludia ani nemyslia.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 29. 10. 2015 23:16
Re: Dokaz iracionality
Možná zajímavější a obecnější otázka, existují celá čísla 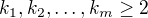 a racionální
a racionální  taková, že pro
taková, že pro 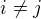 je
je 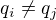 , pro všechna
, pro všechna  nejsou čísla
nejsou čísla ![kopírovat do textarea $\sqrt[k_i]{q_i}$](/mathtex/e8/e8de77877300eee532f009cafc4bbb22.gif) racionální a přitom je racionální číslo
racionální a přitom je racionální číslo  ?
?
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#8 29. 10. 2015 23:41
Re: Dokaz iracionality
Ahoj ↑ byk7:,
To moze byt nova diskuzia, i ked takto polozena otazka zda sa skor tazka.
Urob skor nove vlakno a zacni diskuziu z jednoduchymi situciamy, take ze to mozno vyriesi tvoju otazku ( aj vdaka kolegom).
Co motivovalo tvoju otazku?
Ja som tu polozil ( na opak) jednu otazku, v jednoduchej formulacii. A uz sme napisali riesenia co mozu dat peknu otazku na skusky ...
Mozno z takychto specialnych situacii sa objavi nieco vseobecnejsie.
Na otazku ↑ vanok: nemas aj ty nieco co este nebolo povedane?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 30. 10. 2015 00:14
Re: Dokaz iracionality
↑ vanok:
Moji otázku motivovala zkušenost, že všech úlohách, ve kterých se vyskytoval součet nějakých (řekněme "netriviálních") odmocnin, že tento součet je iracionální. Proto to zobecnění.
Jinak pro  jsem se situaci pokoušel nasoukat na nějaký z důkazů zde (mimo prvního), ale zatím jsem moc uspěšný nebyl. Zítra se zkusím podívat ještě na tu geometrickou možnost.
jsem se situaci pokoušel nasoukat na nějaký z důkazů zde (mimo prvního), ale zatím jsem moc uspěšný nebyl. Zítra se zkusím podívat ještě na tu geometrickou možnost.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#11 30. 10. 2015 13:23
Re: Dokaz iracionality
Ahoj↑ Brano:,
Ano to je zabavne, ze ten isty zapis sa moze mat rozne interpretacie.
Takto je ale legitimne dat taketo otazky aj pri studiu minimalnych polynomov. 😀
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 21. 11. 2015 19:32 — Editoval vanok (25. 11. 2015 11:33)
Re: Dokaz iracionality
Pozdravujem,
Dam tu popis este jednej metody.
Prva vlasnost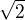 nemoze byt cele, lebo nie je kvadraticke residus
nemoze byt cele, lebo nie je kvadraticke residus 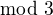
Skutocne, Ak by to tak bolo, tak  pre nejake k cele cislo.
pre nejake k cele cislo.
Tak  , co da
, co da 
Ale to nie je mozne ( staci overit pre 0,1,2), cize je to spor.
Tak 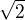 nie je cele cislo.
nie je cele cislo.
Tak mame poucenie : ak urcita vlasnost je je platna mod p ( p premier), tak plati aj pre vsetki cele cisla.
Podobne mame
Ak polynom P ( jednej premennej X) a majuci cele koeficienty. Ak P je irediktibilny na ![kopírovat do textarea $\mathbb{F}[X]_p$](/mathtex/50/50fcaec8396bc6c0d63fd19ceeb25c29.gif) , tak je tiez ireduktibilny na
, tak je tiez ireduktibilny na ![kopírovat do textarea $\mathbb{Z}[X]$](/mathtex/2f/2fc6489512d083678e4ee785fb78d46d.gif) .
.
( opacna implikacia vseobecne neplati)
Co sa da obrazne povedat, ak nejake algebricke cele cislo je lokalne iracionalne, tak musi byt iracionalne.
To nam moze dat myslienku na dokaz napr. Ze 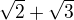 je iracionalne, podrobne ako je to tu vyssie popisane.
je iracionalne, podrobne ako je to tu vyssie popisane.
Na to staci mat prvocislo p, take, ze  je kvadraticke residus
je kvadraticke residus 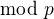 ale zaroven
ale zaroven  nie je kvadraticke residus
nie je kvadraticke residus 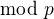 .
.
Polozme  ( k cele cislo), pracujme
( k cele cislo), pracujme 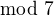 ,
,
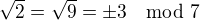 ( tiez mame pochopitelne, ze
( tiez mame pochopitelne, ze  nie je kvadraticke residus
nie je kvadraticke residus 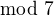 )
)
Co je ekvivalentne z  Ale to je nemozne, cize mame spor.
Ale to je nemozne, cize mame spor.
Cvicenie. Dokaz te podobne, ze  je iracionalne.
je iracionalne.
Iste poznate aj ine metody. Ake?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Dokaz iracionality

 je
je  bud cele, alebo iracionalne.
bud cele, alebo iracionalne. racionalne, tak aj
racionalne, tak aj  je racionalne a teda aj
je racionalne a teda aj 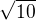 je racionalne a tym padom cele; avsak sa nachadza v intervale
je racionalne a tym padom cele; avsak sa nachadza v intervale 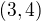 lebo
lebo  a to je spor.
a to je spor. tj
tj 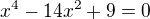 atd. podla toho co si pisal
atd. podla toho co si pisal